主成分分析略讲

Posted on by

主成分分析是为了简化变量的个数。
我这里不涉及到任何高级统计知识来简单讲解一下主成分分析，首先我们用下面的代码随机创造一个矩阵：

options(digits = 2)
x=c(rnorm(5),rnorm(5)+4)
y=3*c(rnorm(5),rnorm(5)+4)
dat=rbind(x,y,a=0.1*x,b=0.2*x,c=0.3*x,o=0.1*y,p=0.2*y,q=0.3*y)
colnames(dat)=paste('s',1:10,sep="")
dat
library(gmodels)
pca=fast.prcomp(t(dat))
pca
summary(pca)$importance
biplot(pca, cex=c(1.3, 1.2));

那么根据我们的创建规则，其实a,b,c,o,p,q变量跟x,y是有关系的，而主成分分析，就是找出这个关系：a=0.1x,b=0.2x,c=0.3x,o=0.1y,p=0.2y,q=0.3y
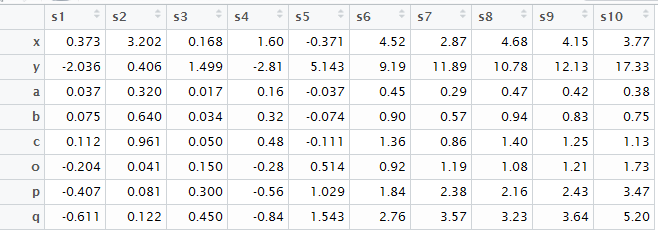
image001

如果不用主成分分析，我们需要把所有的变量进行两两组合，计算量太大了
我们直接gmodels用这个保留里面的函数fast.prcomp来对dat矩阵做主成分分析，分析结果如下：
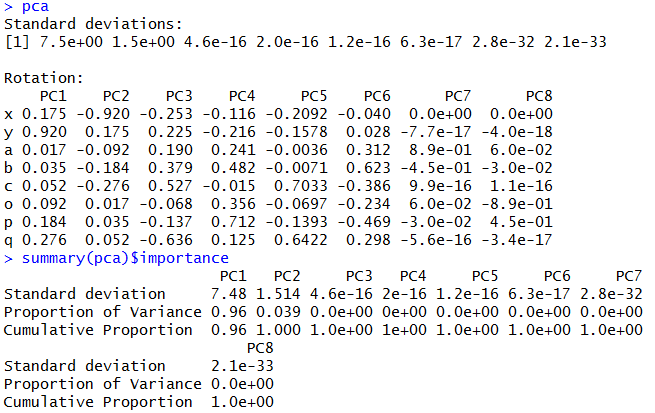
image002
主成分分析就是降维，本来应该有8个变量，现在我们变成了8个主成分，而一般前面的几个主成分就能解释所有的数据了。
比如我们看这个PC1,PC2，根据结果画出下面的图，把我们的矩阵区分的特别清楚。
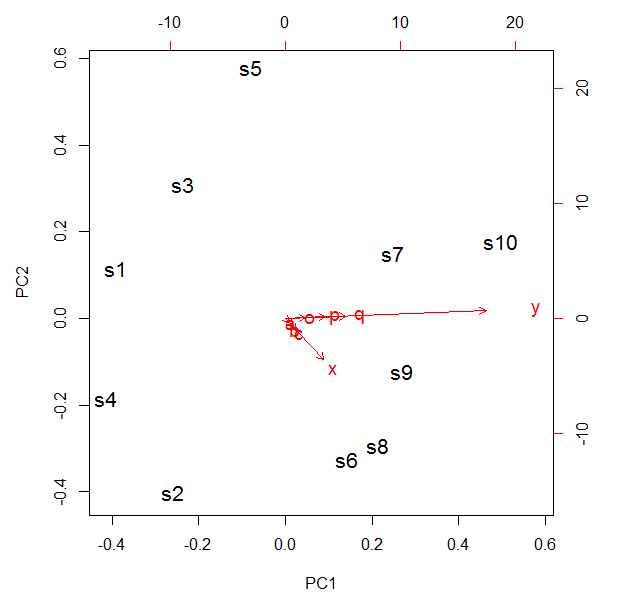
image003
如果想继续了解其中的统计学原理，请自行看下面的ppt
http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf
https://www.cs.princeton.edu/picasso/mats/PCA-Tutorial-Intuition_jp.pdf
http://www.cs.umd.edu/~samir/498/PCA.pdf
http://www.yale.edu/ceo/Documentation/PCA_Outline.pdf
http://people.tamu.edu/~alawing/materials/ESSM689/pca.pdf （R相关）
http://www2.dc.ufscar.br/~cesar.souza/publications/pca-tutorial.pdf （2012）
中文的更多啦，我就不贴地址啦

​

 

Comments are closed.