熵（entropy）在统计学中是一个很重要的概念，代表着信息的多少。经济学里面衡量贫富差距的基尼系数，以及环境生物学领域衡量物种多样性的辛普森多样性指数，以及免疫组库领域的D50都有异曲同工之妙。

基尼系数距离普通人的生活最近，通俗一点来理解：

• 比如有10个人，他们的月薪都是2万，那么这10个人组成的小团体的基尼系数就是0，说明没有贫富差距

• 如果他们的月薪都是3万，基尼系数也仍然是0 ，因为大家都一样。

• 但是如果他们的收入是1到10，每个人不一样，那么这个小团体的基尼系数就是0.3

• 如果前面的9个人是1到9万的收入，但是最后一个月不是10万，而是100万，这个小团体的基尼系数就是0.67
• 如果最后那个人是1个亿，基尼系数就会接近于1。

使用R代码，模拟这样的10个人小团体：

n=3
a=rep(n,10)
b1=a/sum(a)
b1 # 首先每个人的收入都是3万
plot(cumsum(b1),type = 'l')
a=1:10
a=sort(a)
b2=a/sum(a)
b2 ## 然后每个人的收入都不一样，相差一万
points(cumsum(b2),type = 'l')
a=c(1:9,100)
a=sort(a)
b3=a/sum(a)
b3 # 最后，假定其中一个人收入是100万，遥遥领先剩余的9个人
points(cumsum(b3),type = 'l')

y1=as.numeric(table(b1)/length(b1))
y2=as.numeric(table(b2)/length(b2))
y3=as.numeric(table(b3)/length(b3))

如下所示：

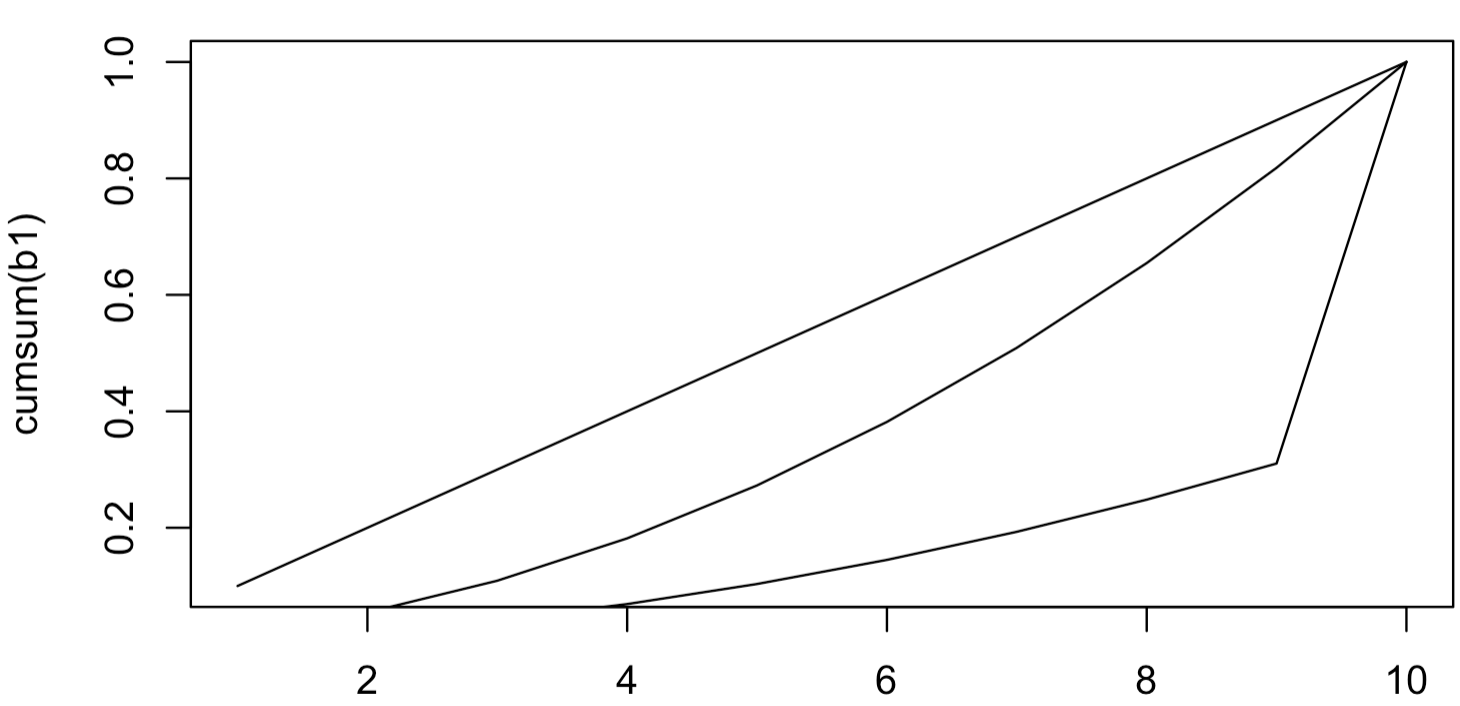
在上图中，10个人，按照收入排序（升序）后，收入累积的占比。

那么，亲爱的读者，你可以猜测一下，我们中国的代表贫富差距的基尼系数是多少？

国际惯例把0.2以下视为收入绝对平均；0.2-0.3视为收入比较平均；0.3-0.4视为收入相对合理；0.4-0.5视为收入差距较大；当基尼系数达到0.5以上时，则表示收入悬殊。

香农信息熵

同样的10个人，同样的月薪都是2万，信息熵就是0，同样的，每个人的收入如果是3万，也不会影响信息熵就是0这个结论。但是如果10个人的收入是1到10万这10种情况，这10个人的信息熵就很大了，是3.32，但是这10个人的收入多少并不影响信息熵的结果，无论是否有一个人收入高达百万或者过亿，这个信息熵都是3.32，代表着这10个人的小团体很不一样。

所以信息熵并不能用来衡量贫富差距哦。有意思的是，如果10个人变成了100个人，同样的收入都不一样，这个时候的信息熵是6.64，也就是说信息熵居然是跟人数有关哦。但是有一个矫正后的香农信息熵，可以抹去人数的影响，代码如下：

R代码函数如下：

# 默认x 是一个群体的,每个人的收入,数值组成的向量
shannon.entropy <-function(x,type='raw'){
 if(type=='raw'){
 myfreqs <- table(x)/length(x) 
 myvec <- as.data.frame(myfreqs)[,2]
 }else{
 myvec=x
 }
 -sum(myvec * log2(myvec))
}
metric.entropy <-function(x,type='raw'){
 if(type=='raw'){
 myfreqs <- table(x)/length(x) 
 myvec <- as.data.frame(myfreqs)[,2]
 }else{
 myvec=x
 }
 -sum(myvec * log(myvec,length(x)))
}
## modify shannon.entropy to metric entropy

其中shannon.entropy函数其范围0<=I(x)<=1,符合直观感受。

> shannon.entropy(b1)
[1] 0
> shannon.entropy(b2)
[1] 3.321928
> shannon.entropy(b3)
[1] 3.321928
> 
> metric.entropy(b1)
[1] 0
> metric.entropy(b2)
[1] 1
> metric.entropy(b3)
[1] 1

也就是说，如果shannon.entropy接近于0，代表信息量很少，接近于1代表信息量大。

辛普森指数

辛普森多样性指数(Simpson index)，描述从一个群落种连续两次抽样所得到的个体数属于同一种的概率。

其公式如下：D=1-∑(Ni(Ni-1))/(N(N-1))，其中Ni为群落中第i种的个体数，N为群落中所有种的个体数。

如群落A，有甲99个，乙1个；群落B，有甲50个，乙50个；易得前者辛普森多样性指数=0.0198，后者希普森多样性指数=0.5000。也就是说辛普森指数越大，物种多样性越丰富，但辛普森指数最大不超过1。

R代码函数如下：

# 默认x 是一个群体的,每个人的收入,数值组成的向量
Simpson.index <-function(x,type='raw'){
 if(type=='raw'){
 myfreqs <- table(x)/length(x) 
 myvec <- as.data.frame(myfreqs)[,2]
 }else{
 myvec=x
 }
 -sum(myvec * log(myvec,length(x)))
 1-sum( myvec ^2)
}

结果如下：

> Simpson.index(b1)
[1] 0
> Simpson.index(b2)
[1] 0.9
> Simpson.index(b3)
[1] 0.9
> Simpson.index(1:100)
[1] 0.99
> Simpson.index(1:1000)
[1] 0.999

值得注意的是辛普森多样性指数和香农信息熵都不关心具体每个人的收入多少，只统计各种收入数值情况在人群出现的频率进行各自公式计算即可。

GINI系数

基尼系数是本来是一个国际通用的经济学概念，用来衡量贫富差距。基尼系数介于0-1之间，基尼系数越大，表示不平等程度越高。

• 基尼系数最大为1，表示居民之间的收入分配绝对不平均，即100%的收入被一个单位的人全部占有了；
• 基尼系数最小为0，表示居民之间的收入分配绝对平均，即人与人之间收入完全平等，没有任容何差异。

假定一定数量的人口按收入由低到高顺序排队，分为人数相等的n组，从第1组到第i组人口累计收入占全部人口总收入的比重

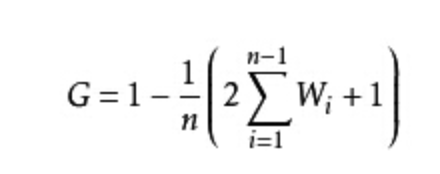
该公式是利用定积分的定义将对洛伦茨曲线的积分(面积B)分成n个等高梯形的面积之和得到的。（看不懂没有关系哈）

R代码函数实现如下：

gini.index <-function(x){ 
 x <- sort(x) 
 G <- sum(x * 1L:length(x)) 
 G <- 2 * G/sum(x) - (length(x) + 1L)
 G/length(x)
}
> gini.index(b1)
[1] 0
> gini.index(b2)
[1] 0.3
> gini.index(b3)
[1] 0.6724138

值得注意的是，基尼系数越下，代表收入越平均，可以理解为多样性越好！

而且基尼系数关心具体每个人的收入情况，换一种说法就是基尼系数与辛普森多样性指数和香农信息熵的输入数据形式其实是不一样的：

• 输入1和2这两个数，来计算香农信息熵结果是1，辛普森多样性指数是0.5；
• 但是对基尼系数来说，输入1和2这两个数，实际上相当于输入了1个a和2个b，就是3个元素。

韩健首创的免疫组库多样性D50

这个D50其实就是饱和度曲线里面的达到50%饱和度，据韩健说是他第一次应用到免疫组库领域。把所有CDR3序列（元素）按照占比比例排序，从最高往最低累加，达到50%的总序列时候的CDR3序列种类比例，就是类似于饱和度曲线。

• D50最大为0.5，意味着全部的CDR3序列占比一致，多样性好；
• D50最小为0，意味着有且只有一种CDR3序列，多样性差。

R代码函数如下：

d50.index <-function(x,type='raw'){
 if(type=='raw'){
 myfreqs <- table(x)/length(x) 
 myvec <- sort(as.numeric(myfreqs),decreasing = T)
 }else{
 myvec=sort(x,decreasing = T)
 }
 len=length(myvec)
 state=cumsum(myvec)>sum(myvec)/2 
 (len -sum(state))/len # 
}

结果如下：

> d50.index(b1)
[1] 0
> d50.index(b2)
[1] 0.5
> d50.index(b3)
[1] 0.5

> d50.index(1:100)
[1] 0.5
> d50.index(1:1000)
[1] 0.5
> d50.index(c(1,2,2,2,3,4))
[1] 0.25

值得注意的是免疫组库多样性D50上限是0.5，因为这个时候人群收入的递减排序，不可能一半的高收入群体居然还达不到全部人群的一半的收入。通常情况是，1%的人就占社会收入的一半了，所以D50通常是0.01甚至更小值。

总结

上面我写的4个公式里面只有基尼系数计算必须输入的是数值，或者把非数值变量取频数后再进行计算。而且仅仅是只有基尼系数是越大，贫富差距越大，多样性越差。其它的数值都是越小多样性越差。

其实，聪明的你，这个时候应该是可以做出来一个总结表格。