我在生信技能树的教程:《你确定你的差异基因找对了吗?》提到过,必须要对你的转录水平的全局表达矩阵做好质量控制,最好是看到标准3张图:
- 左边的热图,说明我们实验的两个分组,normal和npc的很多基因表达量是有明显差异的
- 中间的PCA图,说明我们的normal和npc两个分组非常明显的差异
- 右边的层次聚类也是如此,说明我们的normal和npc两个分组非常明显的差异
如果分组在3张图里面体现不出来,实际上后续差异分析是有风险的。这个时候需要根据你自己不合格的3张图,仔细探索哪些样本是离群点,自行查询中间过程可能的问题所在,或者检查是否有其它混杂因素,都是会影响我们的差异分析结果的生物学解释。
但是最近有学员反馈给我一个表达量芯片数据集: https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE117261
是很经典的的两分组:58 PAH and 25 control lung tissues ,但是如果我们使用默认的无监督的主成分分析来看看这个表达量矩阵的质量情况,会得到如下所示PCA图:
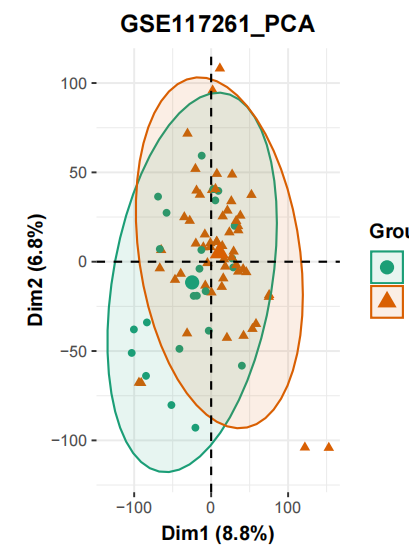
可以很明显的看到,两个分组这个时候区分度并不是很好,值得注意是主成分分析(PCA)是一种无监督学习算法 ,算法尝试从数据中发现模式和结构,而无需预先标记的目标变量。PCA旨在通过找到数据中的主要方差方向来降低数据的维度,从而实现数据的降维和特征提取。 最开始我们的表达量矩阵是两三万个基因在83个样品(58 PAH and 25 control )的表达量信息,以为基因数量实在是太多了,我们很难使用其中的几个或者多个来量化这些样品的距离,所以主成分分析(PCA)就派上了用场,上面的散点图就是可视化了主成分分析(PCA)的前两个主成分。
一般来说,拿到了上面的主成分分析(PCA)图就说明了我们的表达量矩阵里面的3个样品(58 PAH and 25 control )的分组效应并不是最重要的差异来源,后面的两分组的差异分析是有风险的!
gse_number <- 'GSE117261'
gset <- geoChina(gse_number)
a=gset[[1]]
dat=exprs(a) #a现在是一个对象,取a这个对象通过看说明书知道要用exprs这个函数
第1个有监督方案:取差异基因矩阵
首先是提取统计学显著的差异基因,然后针对这些基因构成的表达量矩阵再次进行主成分分析(PCA),代码如下所示 ;
load('GSE117261/anno_DEG.Rdata')
table(DEG$g)
cg = DEG$name[DEG$g!='stable']
load('GSE117261/step1-output.Rdata')
#~~~PCA~~~
exp <- dat[cg,]
## 下面是画PCA的必须操作,需要看说明书。
exp=t(exp)#画PCA图时要求是行名时样本名,列名时探针名,因此此时需要转换
exp=as.data.frame(exp)#将matrix转换为data.frame
library("FactoMineR")#画主成分分析图需要加载这两个包
library("factoextra")
#~~~主成分分析图p2~~~
dat.pca <- PCA(exp , graph = FALSE)#现在exp最后一列是group_list,需要重新赋值给一个dat.pca,这个矩阵是不含有分组信息的
this_title <- paste0(pro,'_PCA')
p2 <- fviz_pca_ind(dat.pca,
geom.ind = "point", # show points only (nbut not "text")
col.ind = group_list, # color by groups
palette = "Dark2",
addEllipses = TRUE, # Concentration ellipses
legend.title = "Groups")+
theme(plot.title = element_text(size=12,hjust = 0.5))
p2
可以看到,这次因为是刻意挑选了那些在两个分组有差异的基因,然后真的这样的表达量矩阵子集进行主成分分析(PCA),所以这两个分组肯定是在图上面是泾渭分明的:
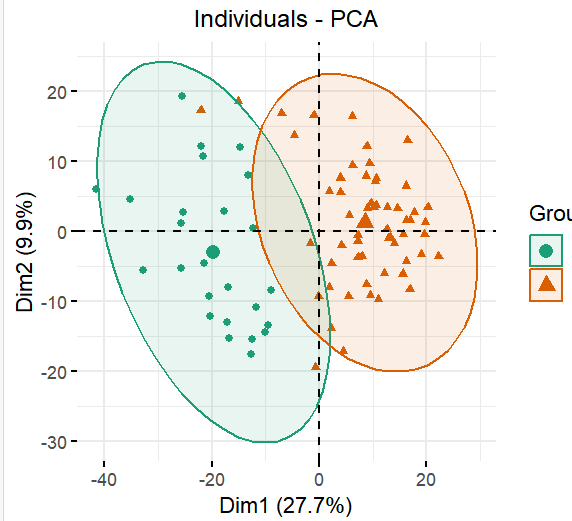
第2个有监督方案:PLS-DA
这里我们使用ropls包 ,这个 是 R 语言中用于多变量数据分析的包,主要用于对高维数据进行统计和可视化分析,特别是用于化学组学和代谢组学数据。ropls 包中包含了一系列的多变量数据分析方法,包括偏最小二乘回归(PLS),主成分分析(PCA),偏最小二乘判别分析(PLS-DA)等。
其中,PLS-DA 是偏最小二乘判别分析,它是一种有监督的学习算法,用于在分类问题中降低多变量数据的维度,并找到最能区分不同类别的方向。与主成分分析(PCA)不同,PLS-DA 依赖于已知的类别信息,因此被归类为有监督学习方法。
无论是上面的pca还是接下来PLS-DA 都是基于表达量矩阵,但是这个时候样品是行,基因是列信息,也就是说我们之前的常规的表达量矩阵被转置了哦,如下所示:
> exp[1:4,1:4]
ABCA10 ABCA8 ABCA9 ABCB1
GSM3290067 4.700215 7.420484 7.363934 3.711399
GSM3290068 4.821179 7.717557 7.747216 3.649032
GSM3290069 5.928191 8.082473 6.985403 3.839583
GSM3290070 5.276074 7.653186 7.152581 6.935727
这个偏最小二乘判别分析(PLS-DA)分析的代码本身就一句话,但是可视化会很耗费时间;
library(ropls)
# 通过orthoI指定正交组分数目
# orthoI = NA时,执行OPLS,并通过交叉验证自动计算适合的正交组分数
oplsda = opls(exp, group_list, predI = 1, orthoI = NA)
## 后面主要是可视化:
library(ggplot2)
library(ggsci)
library(tidyverse)
#提取样本在 OPLS-DA 轴上的位置
sample.score = oplsda@scoreMN %>% #得分矩阵
as.data.frame() %>%
mutate(group = group_list,
o1 = oplsda@orthoScoreMN[,1]) #正交矩阵
head(sample.score)#查看
p <- ggplot(sample.score, aes(p1, o1, color = group)) +
geom_hline(yintercept = 0, linetype = 'dashed', size = 0.5) + #横向虚线
geom_vline(xintercept = 0, linetype = 'dashed', size = 0.5) +
geom_point() +
#geom_point(aes(-10,-10), color = 'white') +
labs(x = 'P1(5.0%)',y = 'to1') +
stat_ellipse(level = 0.95, linetype = 'solid',
size = 1, show.legend = FALSE) + #添加置信区间
scale_color_manual(values = c('#34bfb5','#ff6633')) +
theme_bw() +
theme(#legend.position = c(0.4,0.85),
legend.title = element_blank(),
legend.text = element_text(color = 'black',size = 12, family = 'Arial', face = 'plain'),
panel.background = element_blank(),
panel.grid = element_blank(),
axis.text = element_text(color = 'black',size = 15, family = 'Arial', face = 'plain'),
axis.title = element_text(color = 'black',size = 15, family = 'Arial', face = 'plain'),
axis.ticks = element_line(color = 'black'))
p
可以看到,这个 偏最小二乘判别分析(PLS-DA) 不需要预先对矩阵进行差异分析提取子集,它其实本质上就是尽量在找两个分组的差异然后去可视化这个矩阵里面的样品的距离,那么当然了两个分组就泾渭分明啦:
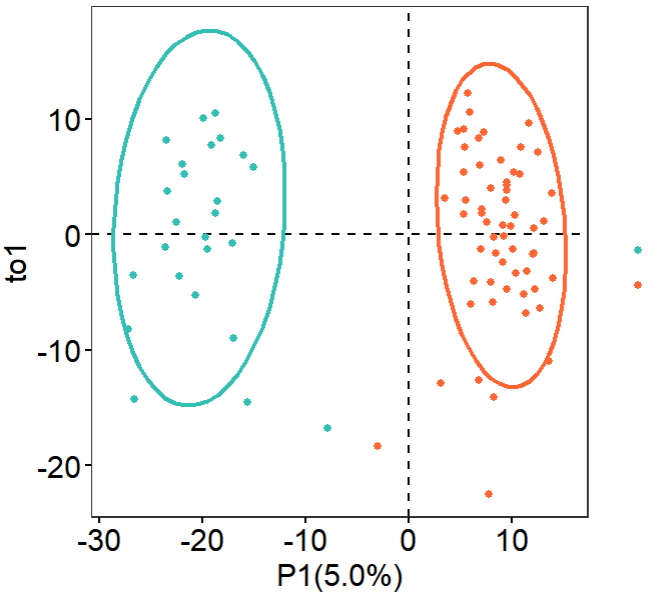
文末友情宣传
强烈建议你推荐给身边的博士后以及年轻生物学PI,多一点数据认知,让他们的科研上一个台阶: