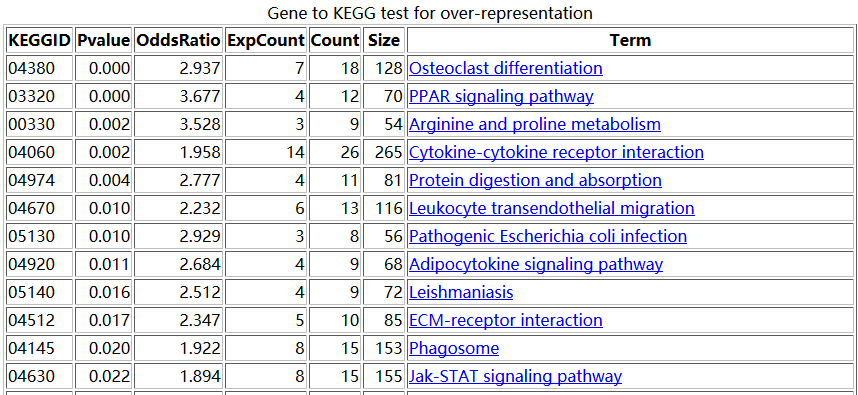
之前我们用超几何分布检验的方法做了富集分析,使用的是GSE63067.diffexp.NASH-normal.txt的logFC的绝对值大于0.5,并且P-value小雨0.05的基因作为差异基因来检验kegg的pathway的富集情况
结果是这样的
我们接下来用另外一种方法来做富集分析,顺便检验一下,是不是超几何分布统计检验的富集分析方法就是最好的呢?
这种方法是-重抽样+主成分分析
大概的原理是,比如对上图中的,04380这条pathway来说,总共有128个基因,那么我从原来的表达矩阵里面随机抽取128个基因的表达矩阵做主成分分析,并且抽取一千次,每次主成分分析都可以得到第一主成分的贡献度值。那么,当我并不是随机抽取的时候,我就抽04380这条pathway的128个基因,也做主成分分析,并且计算得到第一主成分分析的重要性值。我们看看这个值,跟随机抽1000次得到的值差别大不大。
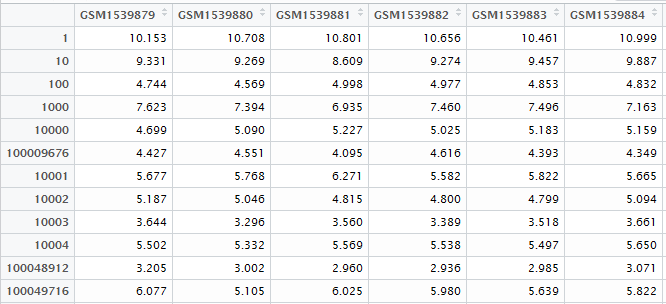
这时候就需要用到表达矩阵啦!
setwd("D:\\my_tutorial\\补\\用limma包对芯片数据做差异分析")
exprSet=read.table("GSE63067_series_matrix.txt.gz",comment.char = "!",stringsAsFactors=F,header=T)
rownames(exprSet)=exprSet[,1]
exprSet=exprSet[,-1]
我们根据ncbi里面对GSE63067的介绍可以知道,对应NASH和normal的样本的ID号,就可以提取我们需要的表达矩阵
把前面两属于Steatosis的样本去掉即可,exprSet=exprSet[,-c(1:2)]
然后再把芯片探针的id转换成entrez id
exprSet=exprSet[,-c(1:2)]
library(hgu133plus2.db)
library(annotate)
platformDB="hgu133plus2.db";
probeset <- rownames(exprSet)
rowMeans <- rowMeans(exprSet)
EGID <- as.numeric(lookUp(probeset, platformDB, "ENTREZID"))
match_row=aggregate(rowMeans,by=list(EGID),max)
colnames(match_row)=c("EGID","rowMeans")
dat=data.frame(EGID,rowMeans,probeset)
tmp_prob=merge(dat,match_row,by=c("EGID","rowMeans"))
relevantProbesets=as.character(tmp_prob$probeset)
length(relevantProbesets) #hgu133plus2.db 20156
exprSet=exprSet[relevantProbesets,]
EGID_name=as.numeric(lookUp(relevantProbesets, platformDB, "ENTREZID"))
rownames(exprSet)=as.character(EGID_name)
d=exprSet
最后得到表达矩阵表格
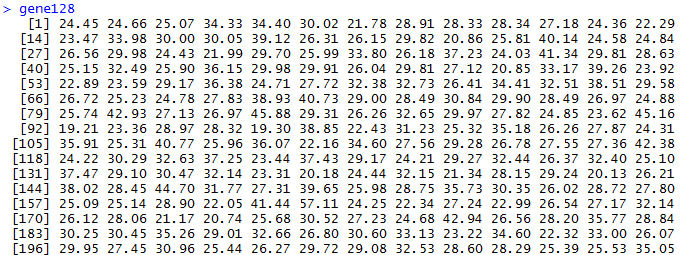
我们首先得到1000次随机挑选128个基因的表达矩阵的主成分分析,第一主成分贡献度值。
gene128=sapply(1:1000,function(y) {
dat=t(d[sample(row.names(d), 128, replace=TRUE), ]);
round(100*summary(fast.prcomp(dat))$importance[2,1],2)
}
)
很快就能得到结果,可以看到数据如下
> summary(gene128)
Min. 1st Qu. Median Mean 3rd Qu. Max.
19.1 25.8 28.8 29.8 32.5 59.7
那么接下来我们挑选这个04380这条pathway特有128个基因来算第一主成分贡献度值
path_04380_gene=intersect(rownames(d),as.character(Path2GeneID[['04380']]))
dat=t(d[path_04380_gene,]);
round(100*summary(fast.prcomp(dat))$importance[2,1],2)
得到的值是38.83,然后看看我们的这个38.83在之前随机得到的1000个数里面是否正常,就按照正态分布检验来算
1-pnorm((38.83-mean(gene128))/sd(gene128))
[1] 0.0625
可以看到已经非常显著的不正常了,可以说明这条通路被富集了。
至少说明超几何分布检验的方法得到的富集分析结果跟我们这次的重抽样+主成分分析结果是一致的,当然,也有不一致的,不然就不用发明一种新的方法了。
如果写一个循环同样可以检验所有的通路,但是这样就不需要事先准备好差异基因啦!!!这是这个分析方法的特点!