http://www.zhihu.com/question/19605599
以前看到过一个赌徒「必胜方法」
有一个广泛流传于赌徒中的“必胜方法”,是关于赌徒悖论极好的说明:一个赌场设有“猜大小”的赌局,玩家下注后猜“大”或者猜“小”,如果输了,则失去赌注,如果赢的话,则获得本金以及0.9倍的利润。 “必胜法”是这么玩的:
(1)押100猜“大”;
(2)如果赢的话,返回(1)继续;
(3)如果输的话则将赌注翻倍后继续猜“大”,因为不可能连续出现“大”,总会有获胜的时候,而且由于赌注一直是翻倍,只要赢一次,就会把所有输掉的钱赢回;
(4)只要赢了,就继续返回(1)。
(1)押100猜“大”;
(2)如果赢的话,返回(1)继续;
(3)如果输的话则将赌注翻倍后继续猜“大”,因为不可能连续出现“大”,总会有获胜的时候,而且由于赌注一直是翻倍,只要赢一次,就会把所有输掉的钱赢回;
(4)只要赢了,就继续返回(1)。
一个朋友说写了程序来验证正确与否,我感觉蛮有趣的,想想自己也学了不少,也应该实践一下啦!
写出程序不难,就一个递归而已,不过是应该用并行计算,不然算的太慢了
另外一个重点是,如何随机???
[R]
judge=function(l=left,c=count,n=number,w=win){
c=c+1;
if(rnorm(1)>0){
l=l+2^n
n=1 # win
w=w+1
}else{
l=l-2^n
n=n+1 #lose
}
return(c(l,c,n,w))
}
my_fun=function(x){
tmp=judge(0,1,1,0)
for(i in 1:x){
tmp=judge(tmp[1],tmp[2],tmp[3],tmp[4])
print(tmp)
}
return(tmp[1])
}
my_fun(10)
c=c+1;
if(rnorm(1)>0){
l=l+2^n
n=1 # win
w=w+1
}else{
l=l-2^n
n=n+1 #lose
}
return(c(l,c,n,w))
}
my_fun=function(x){
tmp=judge(0,1,1,0)
for(i in 1:x){
tmp=judge(tmp[1],tmp[2],tmp[3],tmp[4])
print(tmp)
}
return(tmp[1])
}
my_fun(10)
[/R]
第一个函数是根据现在的状态,接受你的本金,第几次赌了,以及第几次连续下注,最后,你总共赢了多少次,这四个参数,然后随机给一个大小概率,这样你的本金会变化,赌的次数会加1
第二个函数是传入我们需要赌多少次,看结果:
> my_fun(10) [1] -2 2 2 0 [1] 2 3 1 1 [1] 0 4 2 1 [1] -4 5 3 1 [1] 4 6 1 2 [1] 6 7 1 3 [1] 8 8 1 4 [1] 6 9 2 4 [1] 2 10 3 4 [1] 10 11 1 5 [1] 8 12 2 5 [1] 8 如果我们赌11次,可以看到,我最后会剩余8块钱,每次输赢的情况都反应在里面了,可以自己模拟多次看看! 因为我只赌了11次,所以很快,如果我赌1000次,而且还想检验一下10000次模拟结果,就会比较慢了! 我首先使用进度条模拟一下结果,代码如下:还是比较慢的##Time difference of 1.861802 mins 我用了apply,好像时间是节省了一些,不过聊胜于无!
> library(pbapply) > start=Sys.time() > results=pbsapply(1:10000,function(i){my_fun(1000)}) |++++++++++++++++++++++++++++++++++++++++++++++++++| 100% > Sys.time()-start ##9.909524 secs Time difference of 1.301539 mins 那接下来我们分析一下模拟的结果吧
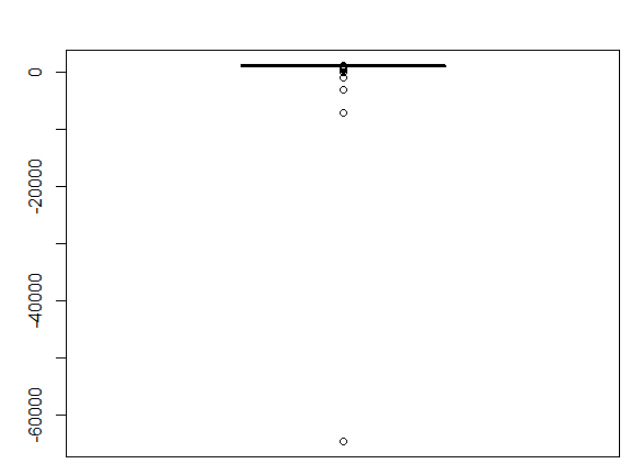
> summary(results) Min. 1st Qu. Median Mean 3rd Qu. Max. -64580 974 998 985 1020 1110 可以看到,我们平均下来是会赢钱的,而且赢面很大,赢的次数非常多!!! 但是,我们看下面的图就知道,一个很诡异的结果! 而且,我这里用的模拟胜负,并不是很好
这其实还只是小批量模拟,如果要模拟百亿次,首先我的笔记本肯定不行,cpu太破了,如果用服务器,就需要用并行计算啦! ##下面是用多核并行计算的代码,大家有兴趣可以自己去玩一下 library(parallel) cl.cores <- detectCores() cl <- makeCluster(cl.cores) clusterExport(cl, "judge") start=Sys.time() results=parSapply( cl=cl, 1:10000, my_fun(1000) ) Sys.time()-start ##4.260994 secs stopCluster(cl)