我们可以直接使用R的bioconductor里面的一个包,GOstats里面的函数来做超几何分布检验,看看每条pathway是否会富集
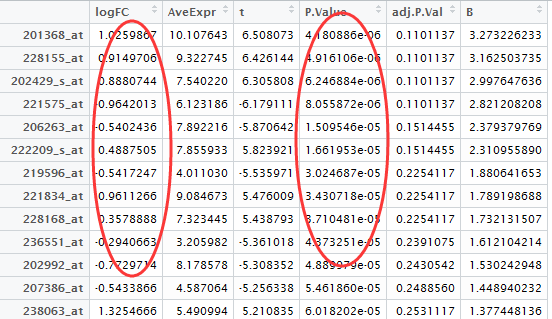
我们直接读取用limma包做好的差异分析结果
setwd("D:\\my_tutorial\\补\\用limma包对芯片数据做差异分析")
DEG=read.table("GSE63067.diffexp.NASH-normal.txt",stringsAsFactors = F)
View(DEG)
我们挑选logFC的绝对值大于0.5,并且P-value小雨0.05的基因作为差异基因,并且转换成entrezID
probeset=rownames(DEG[abs(DEG[,1])>0.5 & DEG[,4]<0.05,])
library(hgu133plus2.db)
library(annotate)
platformDB="hgu133plus2.db";
EGID <- as.numeric(lookUp(probeset, platformDB, "ENTREZID"))
length(unique(EGID))
#[1] 775
diff_gene_list <- unique(EGID)
这样我们的到来775个差异基因的一个list
首先我们直接使用R的bioconductor里面的一个包,GOstats里面的函数来做超几何分布检验,看看每条pathway是否会富集
library(GOstats)
library(org.Hs.eg.db)
#then do kegg pathway enrichment !
hyperG.params = new("KEGGHyperGParams", geneIds=diff_gene_list, universeGeneIds=NULL, annotation="org.Hs.eg.db",
categoryName="KEGG", pvalueCutoff=1, testDirection = "over")
KEGG.hyperG.results = hyperGTest(hyperG.params);
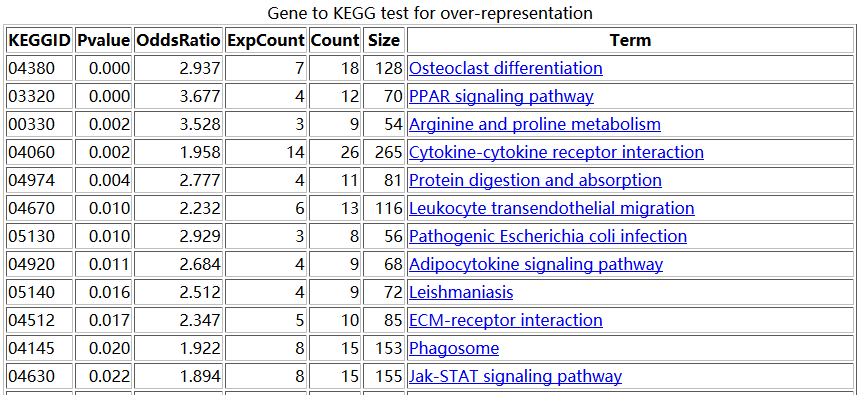
htmlReport(KEGG.hyperG.results, file="kegg.enrichment.html", summary.args=list("htmlLinks"=TRUE))
结果如下:
但是这样我们就忽略了其中的原理,我们不知道这些数据是如何算出来的,只是由别人写好的包得到了结果罢了。
事实上,这个包的这个hyperGTest函数无法就是包装了一个超几何分布检验而已。
如果我们了解了其中的统计学原理,我们完全可以写成一个自建的函数来实现同样的功能。