一．首先加载一些包，这样才能获得该ozone数据

数据集介绍：

Ozone数据集是一个三维数组，记录了24×24个空间网格内，从1995年1月到2000年12月，共72个时间点上，中美洲每月的平均臭氧水平。

前两维分别表示纬度和经度，第三维表示时间。

加载包的代码如下：

library("MASS", lib.loc="C:/Program Files/R/R-3.1.1/library")

library("ggplot2", lib.loc="C:/Program Files/R/R-3.1.1/library")

library("plyr", lib.loc="C:/Program Files/R/R-3.1.1/library")

library("dplyr", lib.loc="C:/Program Files/R/R-3.1.1/library")

library("reshape2", lib.loc="C:/Program Files/R/R-3.1.1/library")

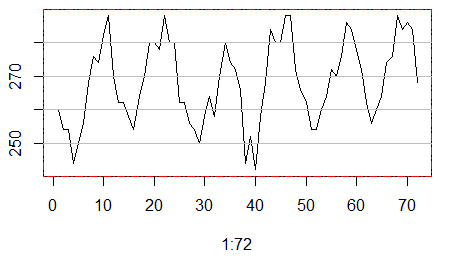
二．我们首先简单看看第一个地点的72个月的臭氧水平变化图。

plot(1:72,ozone[1,1,],type="l")

box(lty = '1373', col = 'red')

grid(nx=NA,ny=NULL,lty=1,lwd=1,col="gray")

看起来还算是蛮有规律的。

三．然后把这72个月的数据分成年份来画图

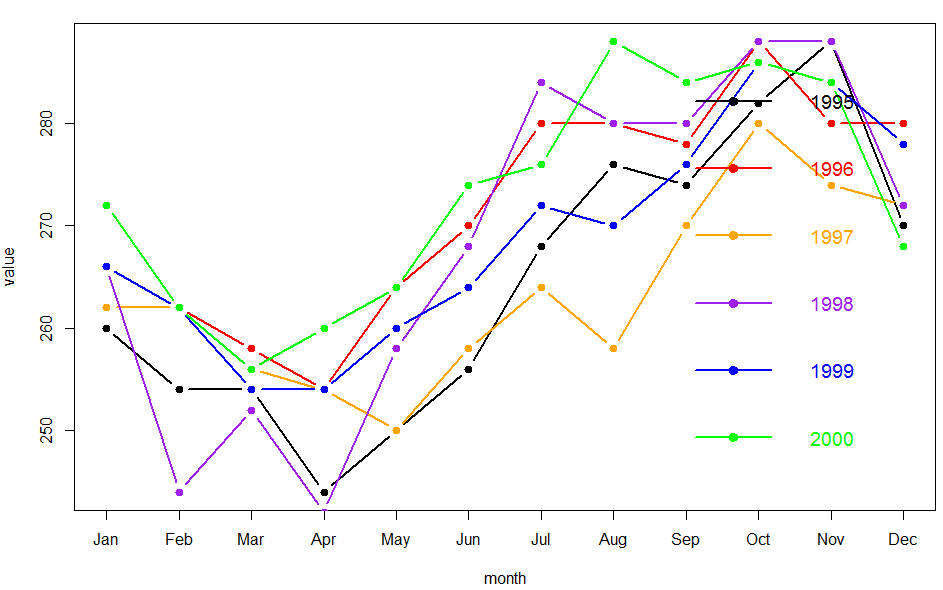
绘图第一种方式如下：

value <-ozone[1, 1, ]

plot(value[1:12],type="b",pch=19,lwd=2,xaxt="n",col="black",

xlab="month",ylab="value")

axis(1,at=1:12,labels=c("Jan", "Feb", "Mar", "Apr", "May",

"Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"))

lines(value[13:24],col="red",type="b",pch=19,lwd=2)

lines(value[25:36],col="orange",type="b",pch=19,lwd=2)

lines(value[37:48],col="purple",type="b",pch=19,lwd=2)

lines(value[49:60],col="blue",type="b",pch=19,lwd=2)

lines(value[61:72],col="green",type="b",pch=19,lwd=2)

legend("bottomright",legend=c("1995","1996","1997","1998","1999","2000"),

lty=1,lwd=2,pch=rep(19,6),col=c("black","red","orange","purple","blue","green"),

ncol=1,bty="n",cex=1.2,

text.col=c("black","red","orange","purple","blue","green"),inset=0.01)

是首先画第一年的，然后逐年添加一条线，然后画图例，算是蛮复杂的。

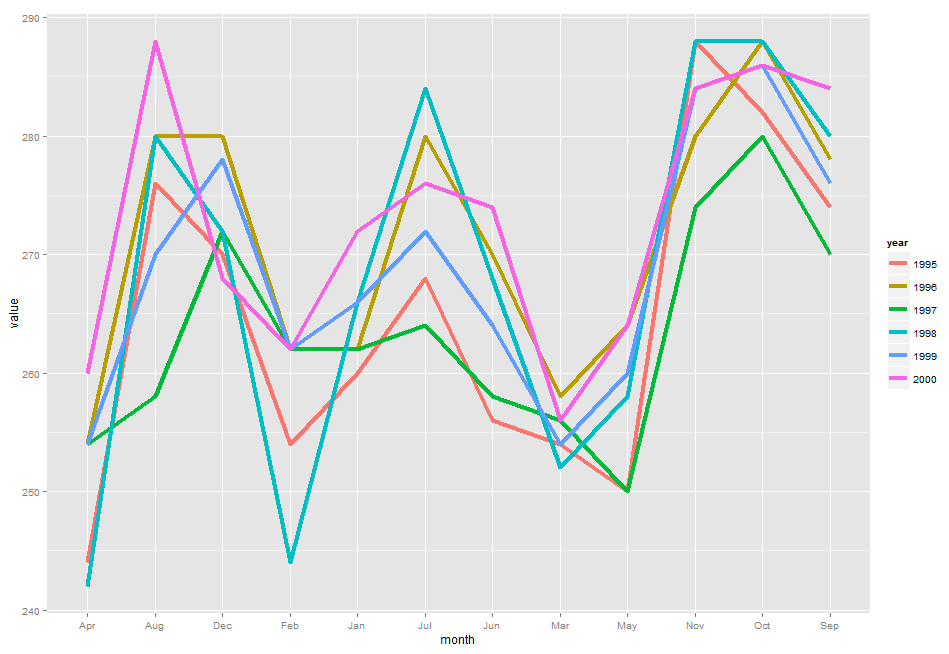
还有一个简单的方法，就是用ggplot这个包来画。

values <-ozone[1, 1, ]

months=c("Jan", "Feb", "Mar", "Apr", "May",

"Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")

years=c("1995","1996","1997","1998","1999","2000")

dat=data.frame(month=rep(months,6),value=values,year=rep(years,each=12))

ggplot(dat,aes(x=month,y=value,group=year,colour=year))+geom_line()

四：测试一下稳健回归模型

稳健回归是加权最小二乘回归，或称文艺最小二乘回归。

MASS 包中的 rlm命令提供了不同形式的稳健回归拟合方式。

回归分析就是用数理统计的方法，研究自然界中变量之间存在的非确定的相互依赖和制约关系，并把这种非确定的相互依赖和制约关系用数学表达式表达出来。其目的在于利用这些数学表达式以及对这些表达式的精度估计，对未知变量作出预测或检验其变化，为决策服务。

介绍几个线性回归（linear regression）中的术语：

残差（Residual）: 基于回归方程的预测值与观测值的差。

离群点（Outlier）: 线性回归（linear regression）中的离群点是指对应残差较大的观测值。也就是说，当某个观测值与基于回归方程的预测值相差较大时，该观测值即可视为离群点。 离群点的出现一般是因为样本自身较为特殊或者数据录入错误导致的，当然也可能是其他问题。

杠杆率（Leverage）: 当某个观测值所对应的预测值为极端值时，该观测值称为高杠杆率点。杠杆率衡量的是独立变量对自身均值的偏异程度。高杠杆率的观测值对于回归方程的参数有重大影响。

影响力点：（Influence）: 若某观测值的剔除与否，对回归方程的系数估计有显著相应，则该观测值是具有影响力的，称为影响力点。影响力是高杠杆率和离群情况引起的。

Cook距离（Cook's distance）: 综合了杠杆率信息和残差信息的统计量。

values <-ozone[1, 1, ]

month.abbr=c("Jan", "Feb", "Mar", "Apr", "May",

"Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")

month_72 <-factor(rep(month.abbr, length = 72), levels = month.abbr)

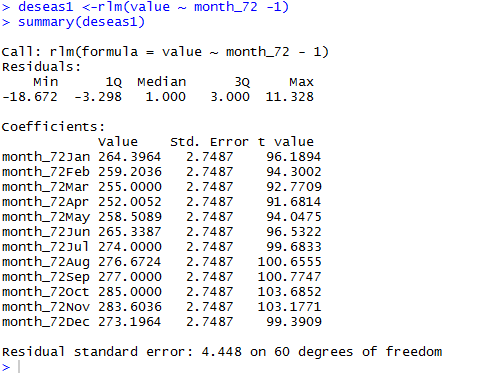
deseas1 <-rlm(value ~ month_72 -1)

summary(deseas1)

五．对我们的24*24个地理位置的数据都做稳健回归分析

deseasf<-function(value) rlm(value ~ month_72 -1, maxit= 50)

models <-alply(ozone, 1:2, deseasf) #model是一个list，储存着24*24次稳健回归的结果

failed <-laply(models, function(x) !x$converged)

coefs<-laply(models, coef)#coefs是一个三维数组，记录了所有24×24个位置中每个位置的12个系数

dimnames(coefs)[[3]] <-month.abbr

names(dimnames(coefs))[3] <-"month"

deseas<-laply(models, resid) #deseas是一个三维数组，记录了所有24×24个位置中每个位置的72个残差

dimnames(deseas)[[3]] <-1:72

names(dimnames(deseas))[3] <-"time"

六．对我们的稳健回归系数的三维矩阵进行降维处理，方便画图

通过reshape包可以对三维数组进行降维

coefs_df<-melt(coefs)

head(coefs_df)

lat   long month   value

1 -21.2 -113.8   Jan 264.3964

2 -18.7 -113.8   Jan 261.3284

3 -16.2 -113.8   Jan 260.9643

4 -13.7 -113.8   Jan 258.9999

5 -11.2 -113.8   Jan 255.9999

6 -8.7 -113.8   Jan 254.9999

可以看到第三维的month成功被降维了

还可以通过plyr这个数据工厂包来进行降维

coefs_df<-ddply(coefs_df, .(lat, long), transform, avg= mean(value), std= value / max(value))

>head(coefs_df)   lat   long month   value     avg       std1 -21.2 -113.8   Jan 264.3964 268.6604 0.92770682 -21.2 -113.8   Feb 259.2036 268.6604 0.90948623 -21.2 -113.8   Mar 255.0000 268.6604 0.89473684 -21.2 -113.8   Apr 252.0052 268.6604 0.88422885 -21.2 -113.8   May 258.5089 268.6604 0.90704866 -21.2 -113.8   Jun 265.3387 268.6604 0.9310129

可以看到，不仅成功降维了，还添加了几个属性变量

 

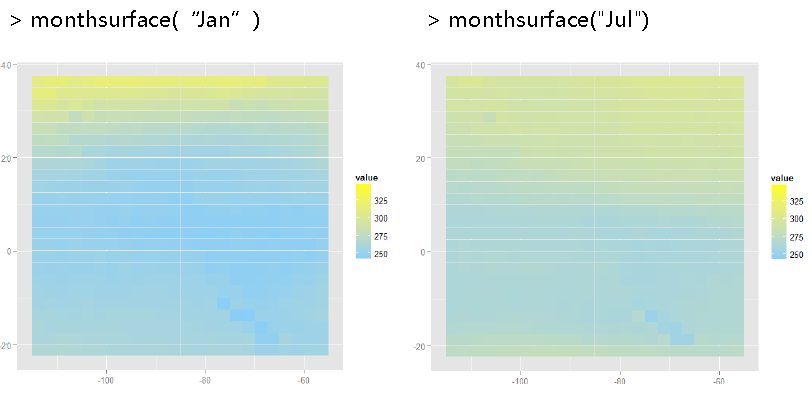
七．最后对降维的coef系数数据画热图

 

coef_limits<-range(coefs_df$value)

coef_mid<-mean(coefs_df$value)

monthsurface<-function(mon)

{

df<-subset(coefs_df, month == mon)

qplot(long, lat, data = df, fill = value, geom="tile") +

scale_fill_gradient(limits = coef_limits,

low = "lightskyblue", high = "yellow")

}

pdf("ozone-animation.pdf", width = 8, height = 8)

l_ply(month.abbr, monthsurface, .print = TRUE)

dev.off()

会在当前R的工作目录下面看到一个pdf文件，里面储存着12个月的在24*24个地理位置的系数热图。