数据分析过程中,检查要用到各种各样的统计学原理。甚至某个原理本身单独都可以讲解一本书。
写在前面
了解生物信息,所有人都绕不开的一部分是统计基础知识和相关实现方式。在这一章中,我们将会简要介绍在实际处理生物数据问题过程中会常碰到统计学概念以及如何使用R语言进行计算和分析。
第一节 描述性统计量
什么是统计学问题呢?通常为了解决一类问题,我们会观察一组和该问题相关的样本,利用总体中的这部分样本来推断总体的情况进而得到结论。在通过样本推断总体之前,我们首先需用对已有样本数据进行简单的评估和描述,针对这一需求也就引出了描述统计量 这一概念。进行描述性统计时,我们最关注的数据两个层面的问题,分别是数据的集中趋势和变异分散性。
数据的集中趋势
面对少则几十个多则上千个数字,第一步通常是观察平均水平。这里介绍三个计算数据平均水平的概念。分别是均值(mean)、中位数(median)和众数(mode)。
均值 :所有观察值的和除以观察的个数。通常,算数平均是最自然和常用的测度,其问题在于对异常值(outliers)非常敏感。有极端值存在时,均值不能代表样本的绝大多数情况。
中位数 :所谓中位数,是指所有样本观测值由小到大排序,位于中间的一个(样本数为奇数)或者两个数据的平均值(样本数为偶数)。
通常,当数据分布对称时,中位数近似等于算数平均数;当数据正倾斜时(画出的图像向右边倾斜),中位数小于算数平均数;当数据负倾斜时(画出的图像向左倾斜),中位数大于算数平均数。因此在很多情况下,我们可以通过比较样本的均值和中位数对数据的分布对称性进行一个初判断。
众数 :在样本的所有观测值中,出现频率最大(出现次数最多)的数值称为众数。这里需要说明的是,当数据量很大而且数值不会多次重复出现时众数并不能给我带来太多的信息。比如当你计算上万个基因的表达量后,得到众数最可能的是0,因为每个基因的表达值或多或少都有一些不同,这时候出现最多的就是那些没有检测的表达基因的0了。
但是在遇到类别数据而非数值型数据时,众数有很大用处,或者说众数是唯一可以用于类别数据的平均数。
在R中,上述提到的均值和中位数可以通过mean(data)和median(data)函数进行计算,而中位数可以通过modeest包的mfv(data)函数得到。
数据的变异性(离散性)
平均数显然不能说明一切问题,因为在说明样本数据时我们还必须考虑数据是不是过于分散。例如在篮球队员的投篮平均得分相同的情况下,更重要的时知道他们哪些人发挥得更加稳定。
极差(range) 指的是一个样本中最大值和最小值之间的差值。在统计学中也称为全距,它能够指出数据的“宽度”(范围)。但是,它和均值一样非常容易受到极端值得影响,而且会受到样本量的明显影响。
针对极差的缺点,统计学中又引入了分位数(quantiles) 的概念,通俗讲就是把数据的“宽度”细分后再去进行比较从而更好地描述数据的分布形态。分位数用三个点将从小到大排列好的数据分为四个相等部分,而这三个点也就是我们常说的四分位数,分别叫做下四分位数,中位数和上四分位数。当然,除了四分位你也可以计算十分位或者百分位。
分位数的引进能够说明数值的位置,但是无法说明某个数值在该位置出现的概率。为了说明数据的稳定程度,我们可以考虑计算每个数据值到平均数的距离(此处,你可以脑补一个高瘦形的数据曲线和矮胖形的数据曲线),但是样本中所有观测值和均值的偏差和永远是0。为了解决这种正负距离相互抵消的问题,统计学中又引入了方差(variance) 和标准差(standard deviation) 的概念。
所谓方差 是指数值与均值距离平方数的平均数,而标准差 则是方差的平方根。标准差体现了数据的变异度,标准差越小,数值和均值越近。通常,均值用μ表示,而标准差用σ表示。
在R中,可以通过quantile()计算分位数,通过var()来计算方差,通过sd()来计算标准差。
有个标准差 的概念,随之而来的问题是当两个样本标准差相同但是均值相差很大时该如何做出区分。统计学中随之引入了变异系数(coefficient of variation, CV) 的概念,变异系数是指样本标准差除以均值再乘100%。变异系数不会受数据尺度的影响,因此常用来进行不同样本之间变异性的比较。
在实际的数据分析中,如果要比较不同数据集(均值和标准差都不同)之间的数值,通常会引入z score 的概念,z score 的计算方法是用某一数值减去均值在除以标准差。通过对原始数据进行z变换,我们将不同数据集转化为一个新的均值为0,标准差为1的分布。
计算描述性统计量
在R中,使用summary()函数方便的得到一个data frame 的各种描述性统计量。当某一列是数值型变量时,你可以得到该列数据的均值、极值、方差和分位数。
下面我们使用R中内置的数据Edgar Anderson’s Iris Data 进行一些简单展示。
Sepal.Length Sepal.Width Petal.Length Petal.Width
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
Median :5.800 Median :3.000 Median :4.350 Median :1.300
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
Species
setosa :50
versicolor:50
virginica :50
形象化展示
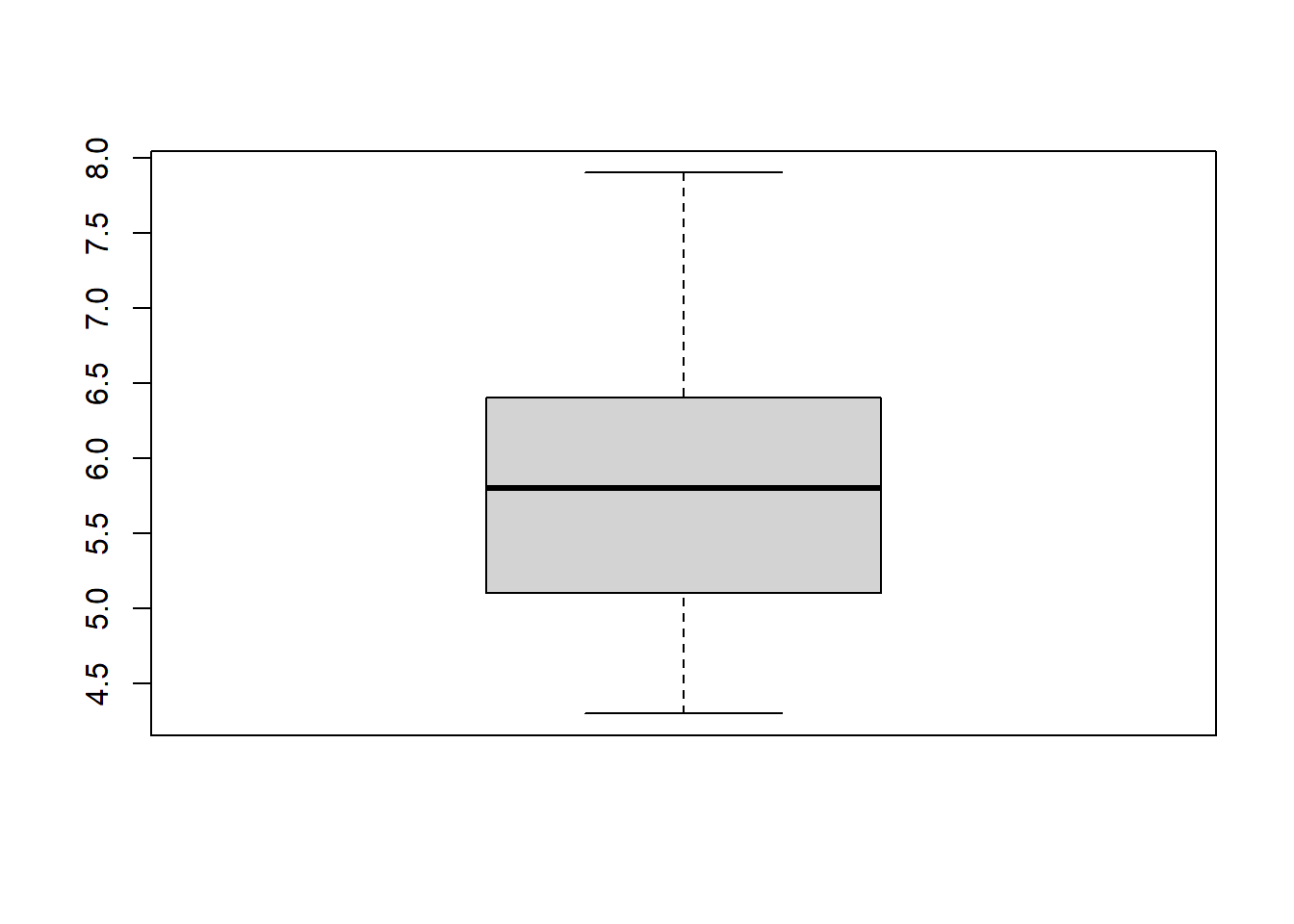
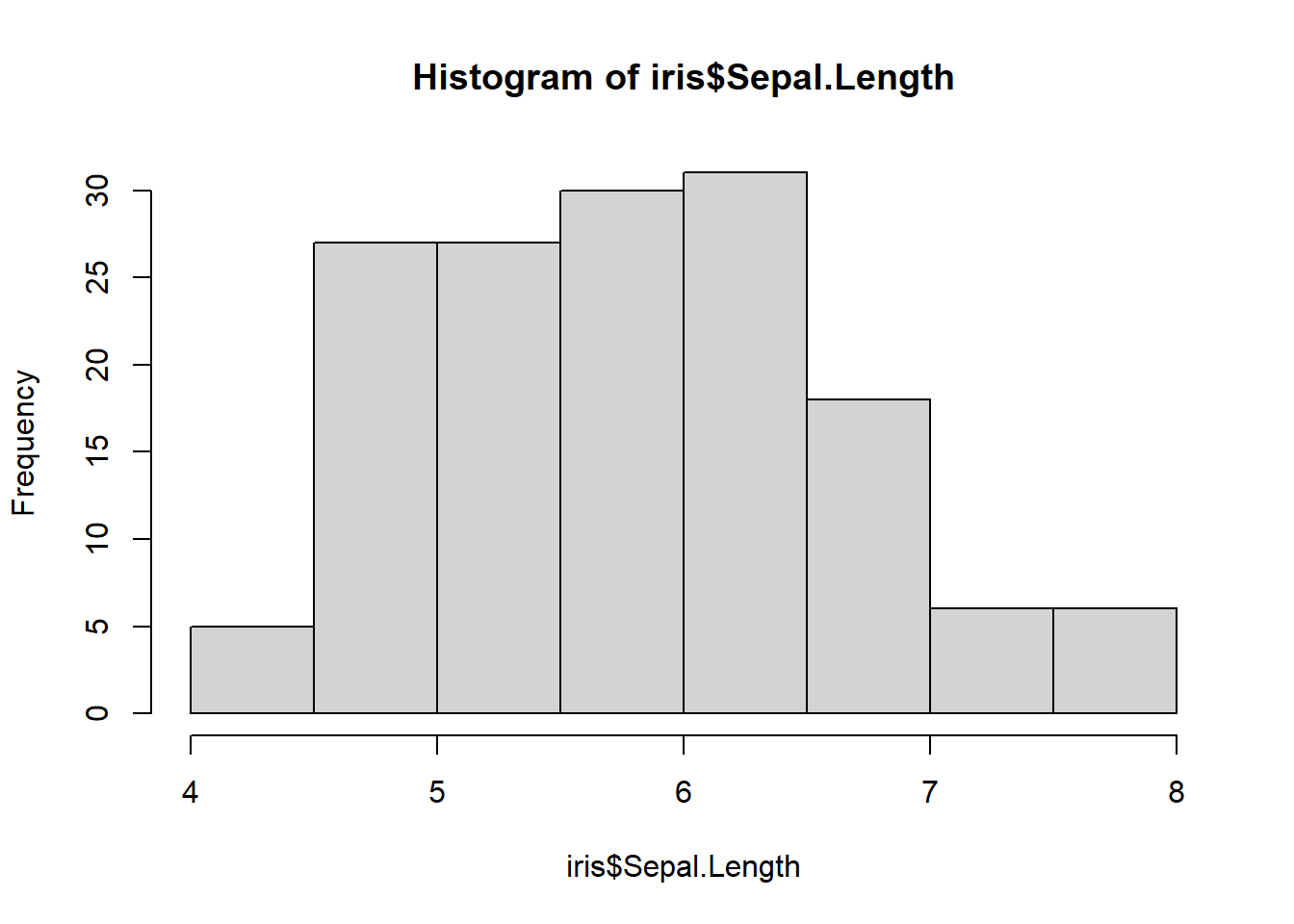
所谓形象化展示就是用图示的方法来展示数据结果,比较常见的方法有条形图,箱线图,直方图等。
boxplot (iris$ Sepal.Length)
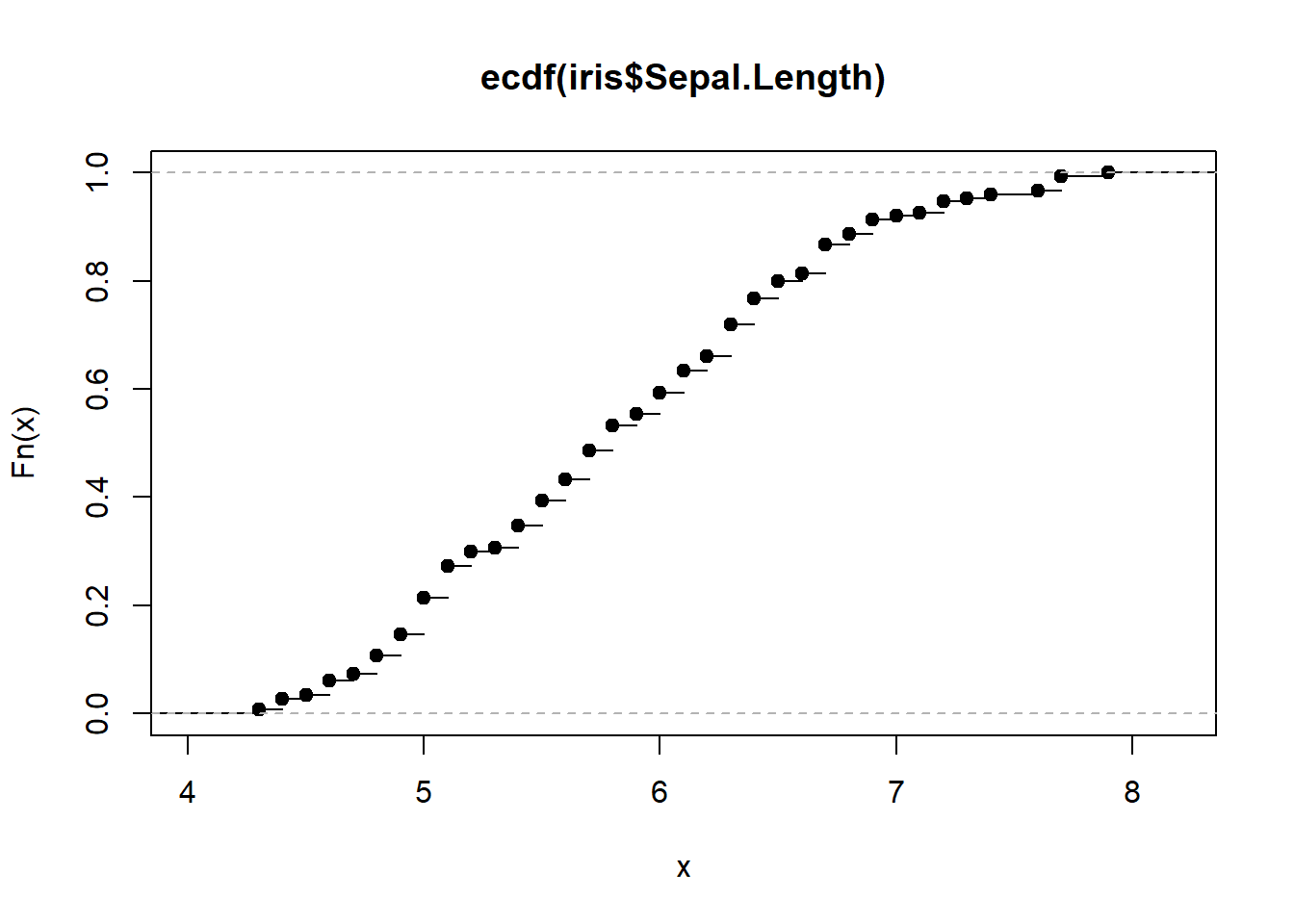
plot (ecdf (iris$ Sepal.Length))# 绘制简单的累积分布函数图展示某一列数据分布情况
第二节 概率相关
统计学中的大量内容源于概率,学习统计学也就必须要了解一些概率中的基本概念,其中尤为重要的是条件概率,以及延伸出的贝叶斯定理(概率论中最牛也是最难掌握的内容之一)。
几个需要理解的概念
样本空间(sample space) 是所有可能结果的一个集合,事件(event) 则是样本空间中所有感兴趣结果的一个子集。某事件的概率(probability) 是该事件在无限次试验次数中的相对频率。
事件的交集并集和补集,概率的加法法则乘法法则在这里不做更加详细的介绍。
条件概率(Conditional Probability) 用来描述与其他事件的发生相关的某个事件的概率,通常被描述成在A事件下发生事件B的概率。在书写过程中用“|”表示,例如P(A|B)就是在B发生的情况下A发生的概率。计算方式为AB同时发生的次数除以所有B发生的次数。
条件概率计算方法:\(P(A|B)=P(A\cap B)/P(B)\)
也可推出 \(P(B|A)=P(A\cap B)/P(A)\) => \(P(A\cap B)=P(A)\times P(B|A)\)
全概率公式:\(P(B)=P(A)\times P(B|A)+P(A')\times P(B|A')\) (贝叶斯定理的分母部分)
贝叶斯定理:\(P(A|B)=\frac{P(A)\times P(B/A)}{P(A)\times P(B|A)+P(A')\times P(B|A')}\)
得到的贝叶斯定理可以帮助我们计算逆条件概率。
在实际的生物学数据处理的过程中,我们还会接触到灵敏度(sensitivity) 、特异度(specificity) 、假阳性(false negative) 和假阴性(false positive) 这几个概念。在疾病方面,对于某一个症状,通俗地说灵敏度指发病后出现症状的概率,特异度不发病时不出现症状的概率。假阳性是指实验结果阳性但是实际为阴性,假阴性是指实验结果为阴性但是实际为阳性。基于灵敏度和特异度,我们经常会看到ROC曲线,通常来说在两个检验中,曲线下面积大的较好。
概率能够告诉我们事件发生的可能性,但如果想要利用概率预测未来的结果并且评估预测的确定性就需要引入概率分布的概念。
离散概率分布
随机变量 : 样本空间中,对不同事件指定有相应概率的数值函数。
随机变量是可以等于一系列数值的变量,这些值又都和一个特定的概率关联。它的写法是P(X=x),表示随机变量X取特定值为x时的概率。随机变量包括离散和连续两种形式,所谓离散指变量只能取一些确定值。连续指的是有无限多种可能取值。
概率分布 也叫概率质量分布,\(P(X=x)\) 。在描述统计量中,样本的频数分布描述每个取值以及对应发生次数,如果样本总数除以对应发生次数,得到的频率分布就类似于这里的概率分布。而所谓的“拟合优度检验”就是比较有限样本频率分布和概率分布的差异。
如果将随机变量和样本对应起来,那么样本中均值的概念在总体(随机变量)中称为期望 ,也叫作总体均值 ,表示为\(\mu\) (和均值一致)或者\(E(X)\) 。计算方式是将每个可能值和概率相乘再把所有乘机相加。和均值类似,这里的期望无法描述相关数值的分散程度。
同样的,在随机变量中也有类似于样本方差的概念,称为总体方差 (随机变量方差),用来表示分散程度。其计算公式为 \(Var(X) = E(X-\mu)^{2}\) 。而概率分布的标准差σ同样是方差的平方根。
计算\(E(X-\mu)^{2}\) 时,首先计算每个数值x的\((x-\mu)^{2}\) ,然后再将结果乘以概率,最后把所有结果相加。
在数据集中,方差和标准差表示的是数据和均值的距离,在概率分布中特定数值概率的分散情况。方差越小,结果越接近期望。
累加分布函数(cumulative-distribution function, cdf) :随机变量X,对于X的任一指定值x,概率值\(P(X\leq x)\) 。即随机变量取值不大于指定值的概率。记作\(F(x)\)
常见的离散概率分布
几何分布 :进行一组相互独立实验,每次实验有成功失败两种可能且每次试验概率相等,想知道第一次成功需要进行的试验次数。 \[P(X=r)=pq^{r-1}\] \[P(X>r)=q^{r}\] \[P(X \leq r)=1-q^{r}\]
期望\(E(X)=\frac{1}{x}\) ;方差 \(Var(X)=\frac{q}{p^{2}}\)
二项分布 :进行一组相互独立试验,每次实验有成功失败两种可能且每次试验概率相等且试验次数有限 ,想知道在有限次试验中成功的次数。 \[P(X=r)=C^{r}_{n}p^{r}q^{n-r}\] 期望\(E(X)=np\) ;方差\(Var(X)=npq\)
二项分布和几何分布差别在于,试验次数固定求成功概率用二项分布,求第一次成功前试验次数用几何分布。
泊松分布 :常与稀有事件相关,单独事件在给定区间(区间可以是时间或者空间)内随机独立发生,该区间内的事件平均发生次数已知且为有限值。这个值用\(\lambda\) 表示。给定区间内发生r次事件个概率计算公式:\[P(X=r)=\frac{e^{-\lambda}\lambda^{r}}{r!}\] 期望是给定区间内能够期望的事件发生次数λ,方差也是λ。如果一个离散随机变量的一批数据计算后方差和均值近似相等,则可以推测样本符合泊松分布。
当二项分布的p很小且n非常大时,\(npq\approx np\) ,方差和期望近似相等,可以用泊松分布来近似二项分布,从而使计算简化。通常,n大于50且p<0.1时为典型的近似情况。
连续概率分布
当数据是连续分布时,人们关心的是取得某一个特定范围的概率。
概率密度函数(probability density function, pdf) :本质是一个函数,用这个函数可以求出在一个范围内的某连续变量的概率,同时该函数可以指出该概率分布的形状。换句话讲,任意a,b两点之间及函数对应曲线下组成的面积等于随机变量X落在ab间的概率。曲线下面积总和是1。
所谓概率密度可以指出各种范围内的概率大小,用面积来表示。只是表示概率的一种方法而非概率本身。
累加分布函数 a点上的值等于随机变量X取值\(\leq a\) 的概率,也是概率密度函数a左边曲线下的面积。
正态分布 是连续数据的一种理想状态。正态分布的概率密度函数是一条对称的钟形曲线,均值具有最大的概率密度,偏离均值概率密度越小。参数μ是均值,也是曲线的中央位置,\(\sigma\) 表述曲线的胖瘦。
连续随机变量X符合均值为μ,标准差为\(\sigma\) 的正态分布时写作\(X\sim N(\mu,\sigma^{2})\) .
线性变换\[aX+b \sim N(a\mu +b,a^{2}\sigma^{2})\] 当X和Y相互独立 (彼此之间没有影响)时: \[X+Y \sim N(\mu_{x}+\mu_{y},\sigma_{x}^{2}+\sigma_{y}^{2})\] \[X-Y \sim N(\mu_{x}-\mu_{y},\sigma_{x}^{2}+\sigma_{y}^{2})\] 期望\(E(X_{1}+X_{2}+...+X_{n})=nE(X)\) ;方差\(Var(X_{1}+X_{2}+...+X_{n})=nVar(X)\)
当X和Y并不彼此独立时,使用协方差(Covariance) 来描述两个随机变量间的关系,记做Cov(X,Y) \[Cov(X,Y)=E[(X-\mu_{x})(Y-\mu_{y})]\]
二项分布正态近似 :通常情况,当二项分布满足\(np\geq 5\) (也有建议\(npq\geq 5\) )时,可以用正态分布代替二项分布。其中\(\mu = np\) ,\(\sigma^{2}=npq\) 。另外,当泊松分布的λ>15时,也可以用正态分布进行近似。
第三节 估计
在通常的试验中,我们获得的信息同时从样本中获得的。想要知道总体参数,只能通过以后样本的参数进行估计。
样本均值是总体均值的点估计。通常,样本均值是用\(\overline x\) 表示,总体均值用\(\mu\) 表示。
在估计总体方差\(\sigma^2\) 时,计算公式为:\[\sigma^2=\frac{\Sigma(x-\overline x)^2}{n-1}\]
用样本方差估计总体方差会使得估计结果偏低,样本越小,两个方差的差别可能就越大。在这里,估计总体方差的公式除以\(n-1\) ,更接近总体方差。另外,总体方差点估计公式通常记做\(s^2\) ,写作:\[s^2=\frac{\Sigma(x-\overline x)^2}{n-1}\]
用样本均值估计总体均值时会产生误差,均值的标准误差是\(\sigma/\sqrt{n}\) ,估计量是\(s/\sqrt{n}\) 。标准误差表示样本均值的分散情况,从公式中我们可以看出,n越大,用样本均值估计总体均值越准去。当样本足够大(大于30)时,即便总体不符合正态分布,但从中取出的样本均值分布仍然近似于正态分布(中心极限定理)。\(\overline X\) ~\(N(\mu, \sigma^2/n)\)
除了对总体进行点估计以外,我们往往还会对总体进行区间估计,即对通过点估计得到的结果加减一定范围的误差。
第四节 相关性分析
本节提到的相关性分析以及后面会提到的t-test, ANOVA 以及回归分析被称为参数检验,这些检验在进行时我们都默认数据符合某种分布,我们的数据符合一定前提条件,通常包括数据符合正态分布和方差相等。当样本数量大于30的时候,根据中心极限定理,我们通常认为数据符合正态分布。在进行t-test和ANOVA分析时,还需要满足样本方差相等条件。
在进行各种检验之前往往需要初步检验一下数据是否符合某种检验的前提条件,如果不符合则应该考虑使用非参数检验等其他方法。
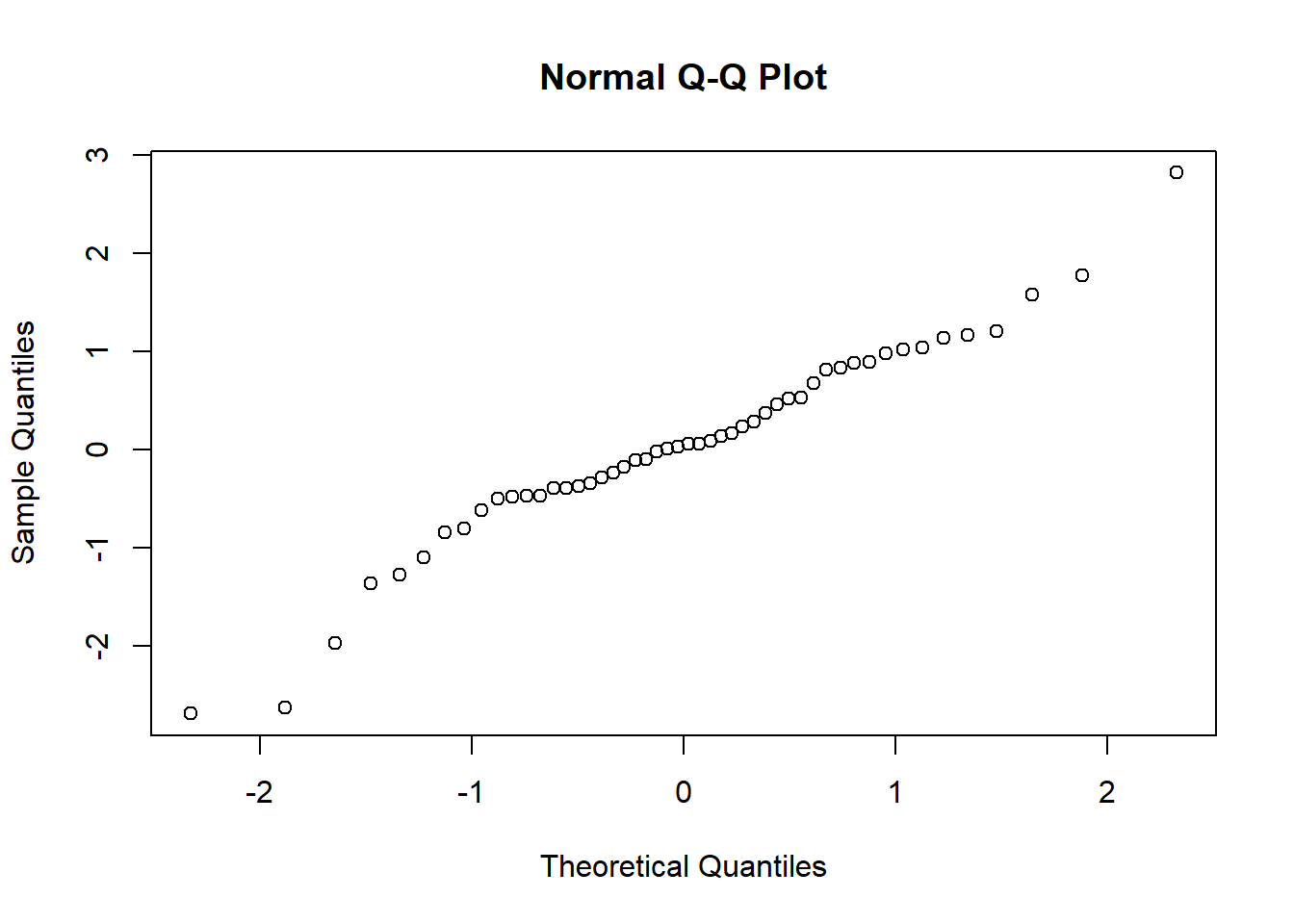
正态分布评估
在评估数据集是否符合正态分布时通常会采用** Shapiro-Wilk’s test**和图示(Q-Q plot)结合的方法。使用Q-Q plot(quantile-quantile plot)的结果比较直观,使用Shapiro-Wilk’s test显著性检验的方法更加准确(相对而言)。
Shapiro-Wilk’s test 结果受样本量的影响非常大,当样本量很大时,即便数据符合正态分布也容易出现p值很小进而拒绝原假设的情况(该检验原假设是样本来自于正态分布)。样本量很小时,即便真实数据不符合正态分布,也可能接受原假设。
这里试举一例
# 分别随机生成两组二项分布和指数分布随机数 set.seed (90 )<- rbinom (15 ,8 ,0.7 )<- rexp (15 ,0.5 )shapiro.test (x)
Shapiro-Wilk normality test
data: x
W = 0.95996, p-value = 0.6917
Shapiro-Wilk normality test
data: y
W = 0.96168, p-value = 0.7216
可以发现即便我们生成的两个样本都不是正态分布,但是检验的结果仍然没有拒绝原假设(没有拒绝不等于接受原假设)。
好在R中这个函数限制了检测的样本个数,3到5000。因此,同时结合图像来看还是很必要的。
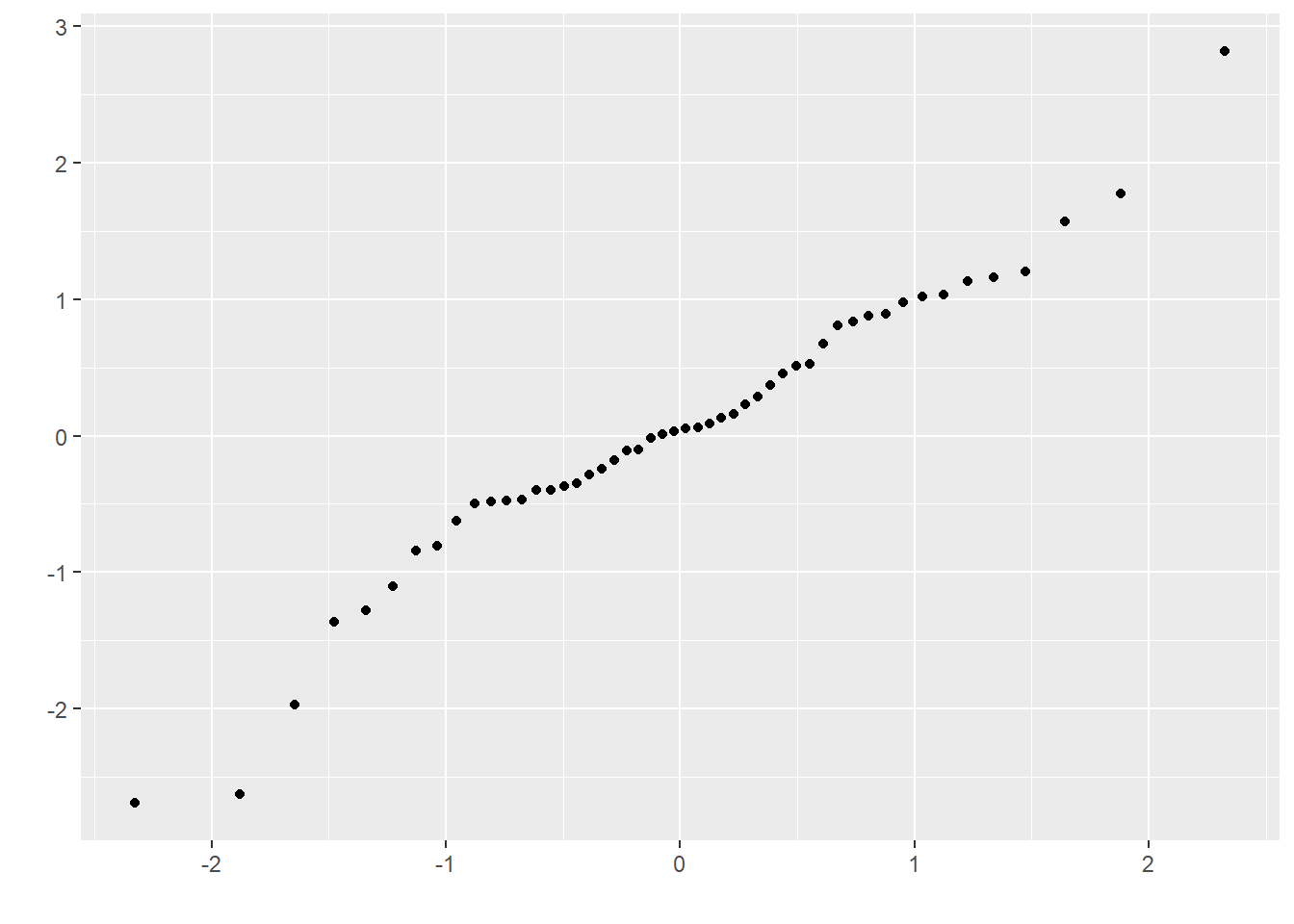
一般使用qqplot来检验是否符合正态分布,R中默认的函数是qqnorm(),ggplot2中可以使用函数qplot(),qqpubr包是基于ggplot2的简易升级版,操作更加友好,可以使用函数ggqqplot()。
下面利用生成的数据绘图。
# 生成符合正态分布的一组数据并绘图 <- rnorm (50 )qqnorm (z)library (ggplot2)
Warning: package 'ggplot2' was built under R version 4.2.3
Warning: `qplot()` was deprecated in ggplot2 3.4.0.
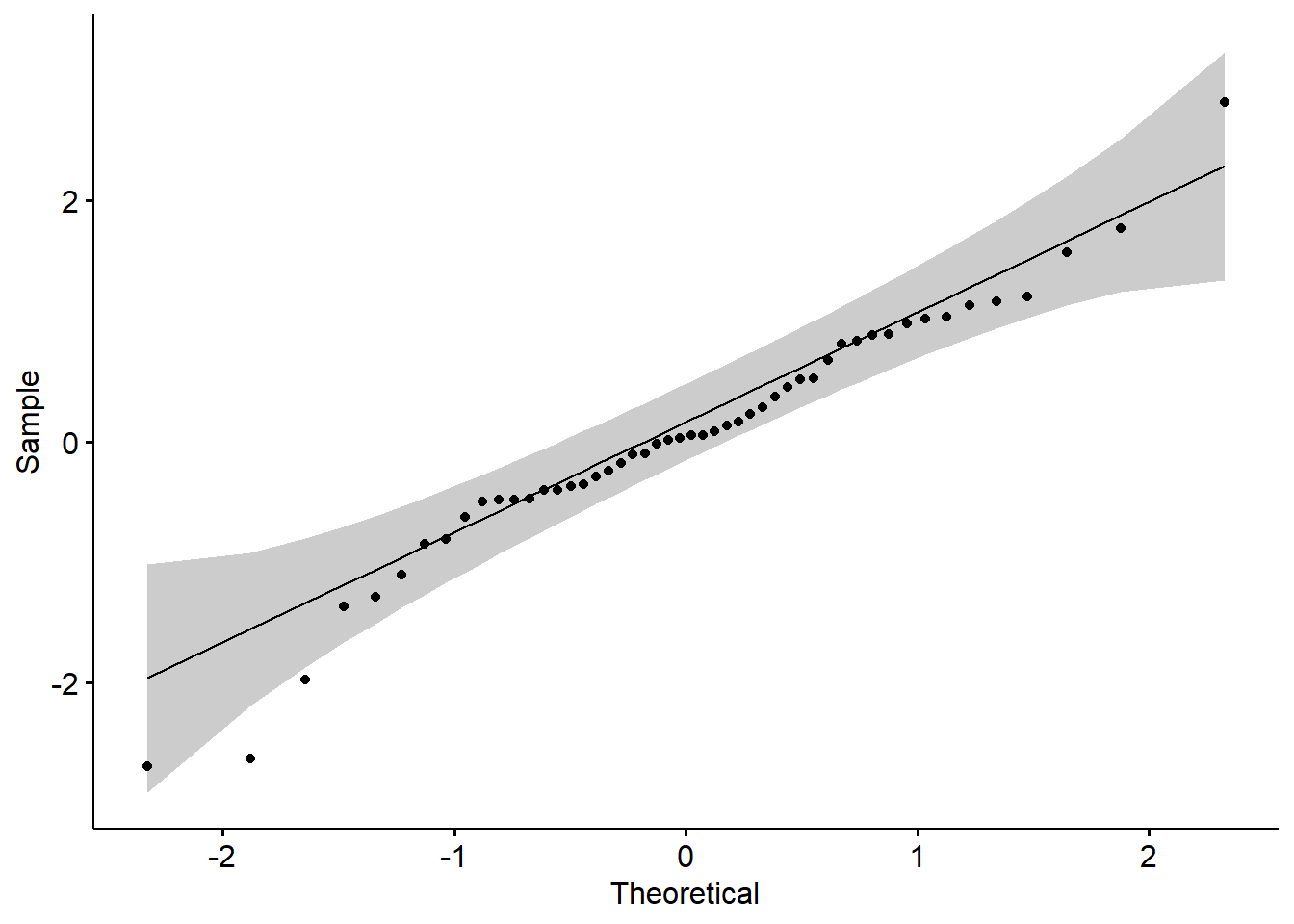
library (ggpubr)ggqqplot (z)
相关性分析
Pearson相关系数、Spearman相关系数、Kendall相关系数都可以用来表示变量之间的相关性,一般情况下,使用pearson相关系数更多,如果比较明确样本不符合正态分布的时候可以使用kendall或者spearman相关系数。这三种相关系数都可以通过cor()函数来进行计算。下面通过R已有数据集cars,查看汽车车速和刹车距离之间的相关性。
pearson相关系数计算公式 \[r = \frac{\sum{(x-m_x)(y-m_y)}}{\sqrt{\sum{(x-m_x)^2}\sum{(y-m_y)^2}}}\] 其中m表示均值。
cor (cars, method = "pearson" )
speed dist
speed 1.0000000 0.8068949
dist 0.8068949 1.0000000
相关性可视化展示
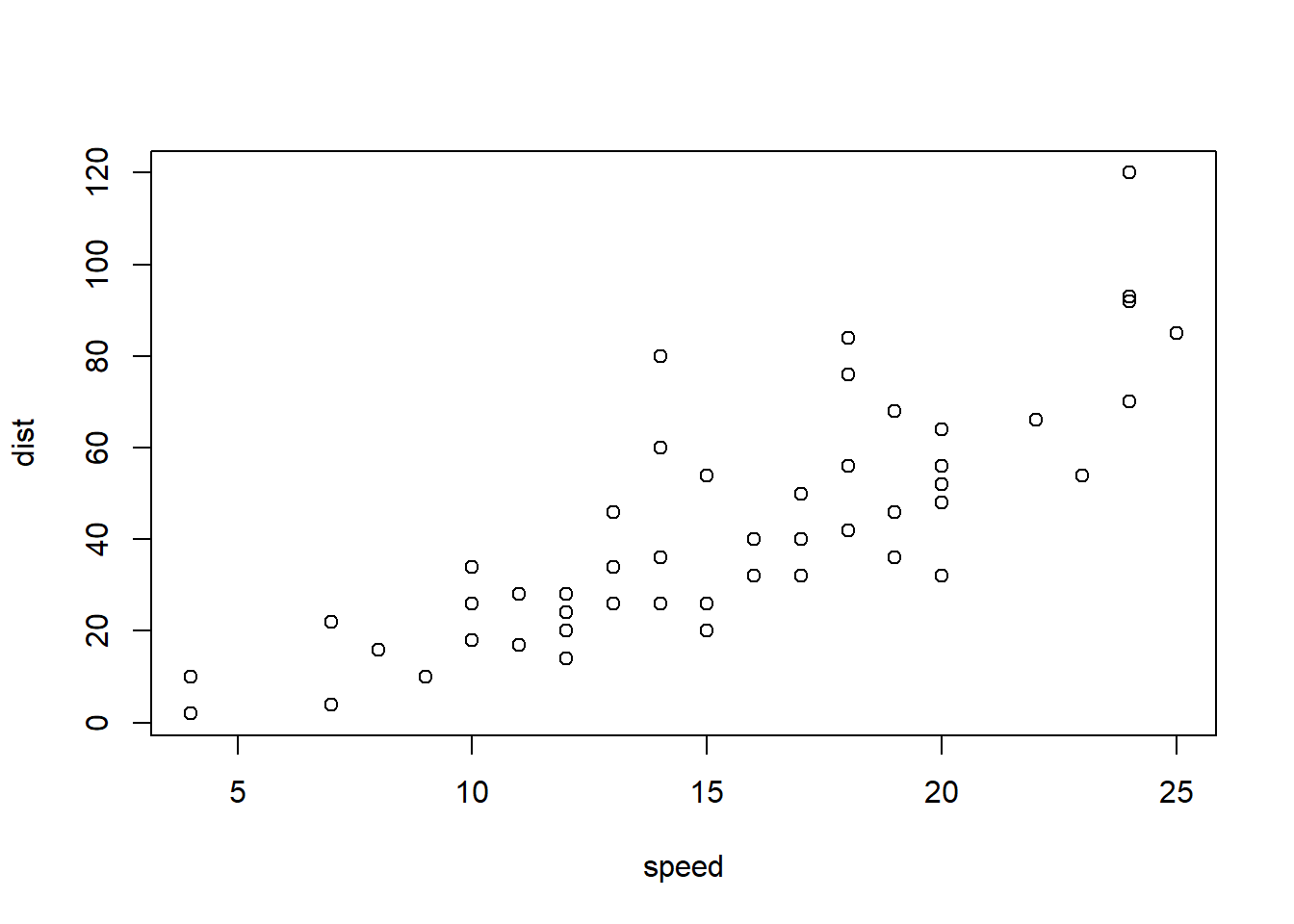
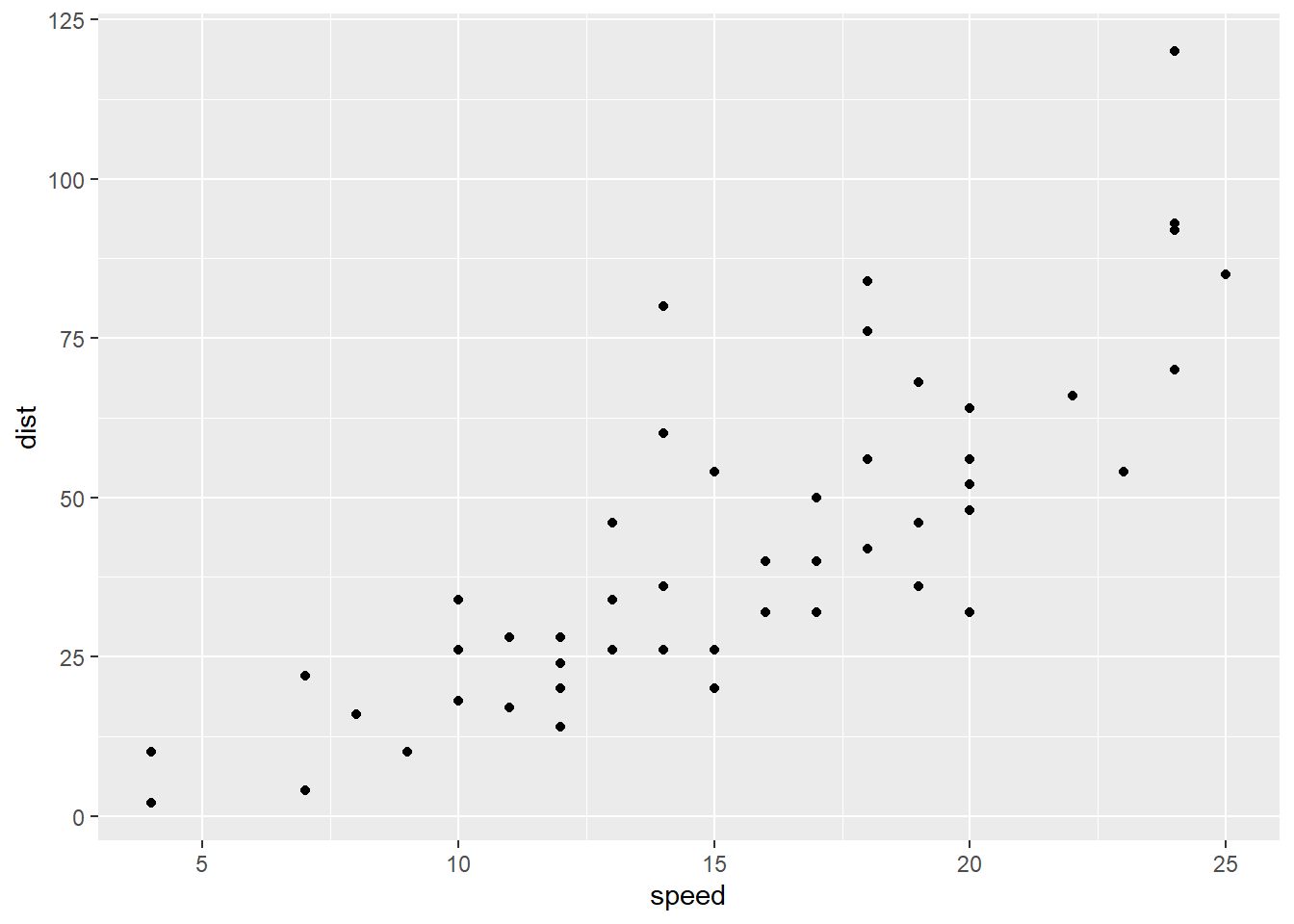
可以使用散点图进行两个变量之间的相关性展示。
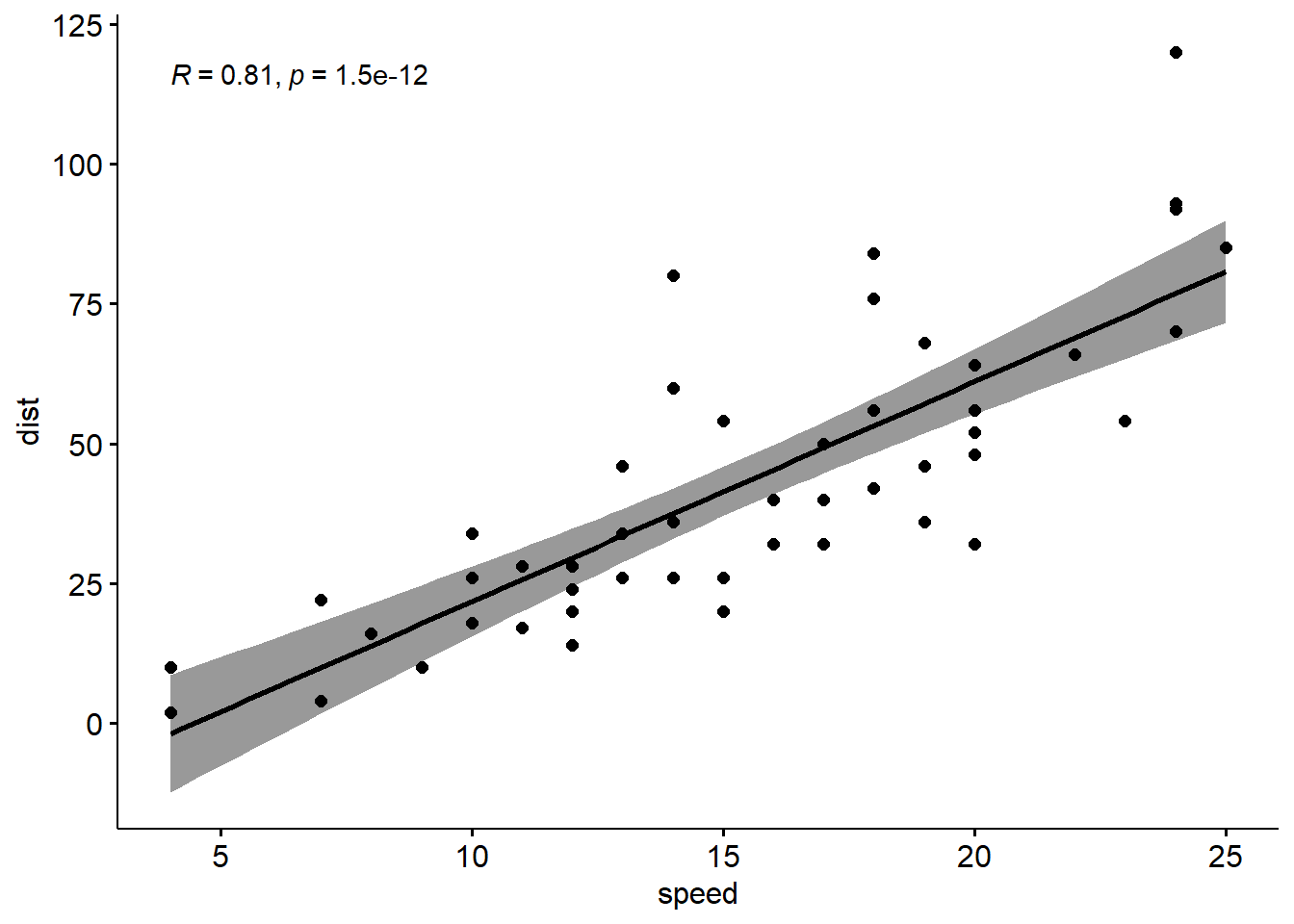
ggplot (cars, aes (x= speed, y= dist))+ geom_point ()ggscatter (cars,x= "speed" , y= "dist" ,add = "reg.line" , conf.int = T,cor.coef = T)
Pearson 相关性检验
前面我们只是计算了两个变量之间的相关性,还应该对相关进行显著性检验。原假设为变量之间没有相关性,使用函数为cor.test()
cor.test (cars$ speed,cars$ dist,alternative = "two.side" , method = "pearson" )
Pearson's product-moment correlation
data: cars$speed and cars$dist
t = 9.464, df = 48, p-value = 1.49e-12
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.6816422 0.8862036
sample estimates:
cor
0.8068949
统计结果中,t表示t检验值,df表示自由度,pvalue是t检验的显著性水平,conf.int表示95%的置信区间,sample estimates 是相关系数。相关系数越接近-1表示负相关,接近1表示正相关。
常用可视化工具
R绘图系统
这部分内容主要从总体上介绍R的两大作图系统:传统绘图系统和grid绘图系统。尽管这部分不会详细介绍如何去绘制某一种具体的图形,但是了解这部分知识却能帮助你在日后作图时根据需求修改已有的绘图工具。
无论是传统绘图系统还是grid绘图系统,它们都是建立在grDevices包的基础上。grDevices被称之为绘图引擎,提供了一系列R中的基本绘图函数,负责绘图参数和图片输出,并且几乎所有的高级的绘图函数都是建立在它的基础上。虽然它如此重要,功能十分强大,但由于太过底层,一般只有R包开发者才会深入研究。建立在绘图引擎之上,有两套互不相容的绘图包:graphics 包和 grid 包,将R的绘图功能从主体上一分为二。
传统绘图系统 :graphics包之所以称其为传统绘图系统,是因为它实现了很多S语言(S语言由贝尔实验室开发并投入商用)所使用的绘图工具,比如说能用于绘制散点图和条形图的plot(),能用于绘制饼图的pie(),能用于绘制条形图的barplot(),而且每一个作图函数都提供了大量的图形参数用于修改图形。我们可以通过library(help="graphics")查看有哪些绘图函数,使用demo("graphics")了解传统绘图系统能绘制哪些图形。
GRID绘图系统 : grid包与传统绘图系统不同,它不负责提供完整的图形函数。它的强大之处在于提供了基于视图概念 定位区域的强大能力,相当于将R变成了Photoshop,也就是意味着你可以将图形视为不同区域元素的叠加,也意味着你可以做出非常复杂的图形,比如说下图
library (grid)grid.newpage ()grid.circle (x= seq (0.1 ,0.9 ,length= 100 ),y= 0.5 + 0.4 * sin (seq (0 ,2 * pi,length= 100 )),r= abs (0.1 * cos (seq (0 , 2 * pi, length= 100 ))))
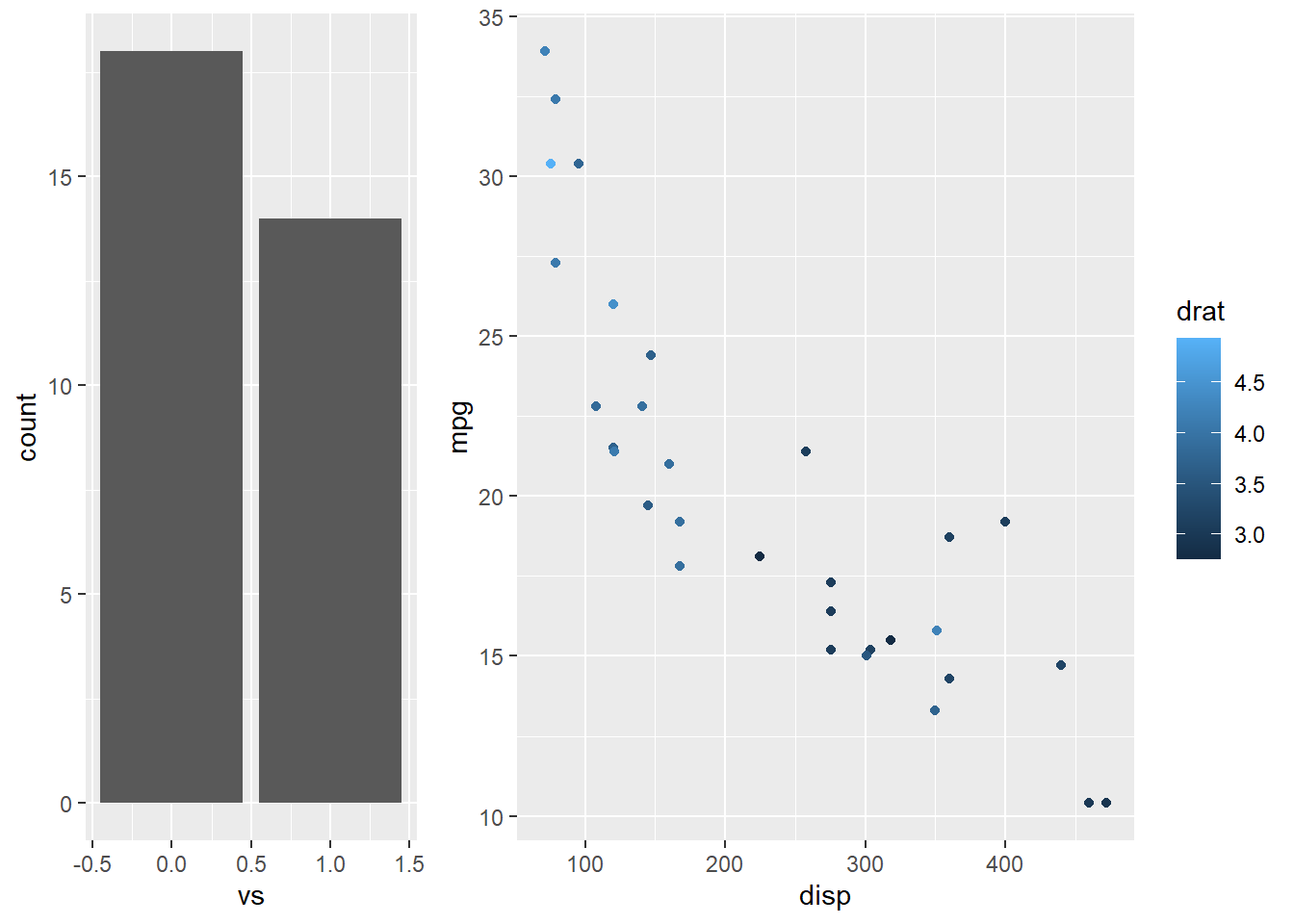
不过人们基本上不会直接使用grid绘制统计图形,一般是采用基于画笔系统 的lattice包或基于图形语法 的ggplot2。 你或许会问,“知道lattice和ggplot2是基于grid对今后作图由什么帮助吗?”。这里就谈及一点,你可以使用grid定制ggplot2输出,也就是将多幅图形集中在一起.
library (ggplot2)grid.newpage ()pushViewport (viewport (x= 0 , width= 1 / 3 , just= "left" ))print (ggplot (mtcars, aes (x= vs)) + geom_bar (),newpage= FALSE )popViewport ()pushViewport (viewport (x= 1 / 3 ,width= 2 / 3 , just= "left" ))print (ggplot (mtcars, aes (x= disp, y= mpg)) + geom_point (aes (color= drat)),newpage= FALSE )
以上仅仅R语言图形系统的简单介绍,如果你只是想要绘制简单的图形,你只要继续看如何通过Google来使用ggplot2可视化 这一篇就够用了。但是如果你希望用R,而不是PS和AI,去随心所欲绘制出任何图形,那么你需要至少看完如下3本书:
可视化举例
表达矩阵可视化大全
无论是芯片数据,还是高通量测序,结果总能得到每个样本的基因表达量数据。而将这些数据导入到R语言,就能得到一组表达量矩阵。对于这组数据,至少可以绘制如下图形
箱形图(boxplot)
小提琴图(vioplot)
柱状图(histogram)
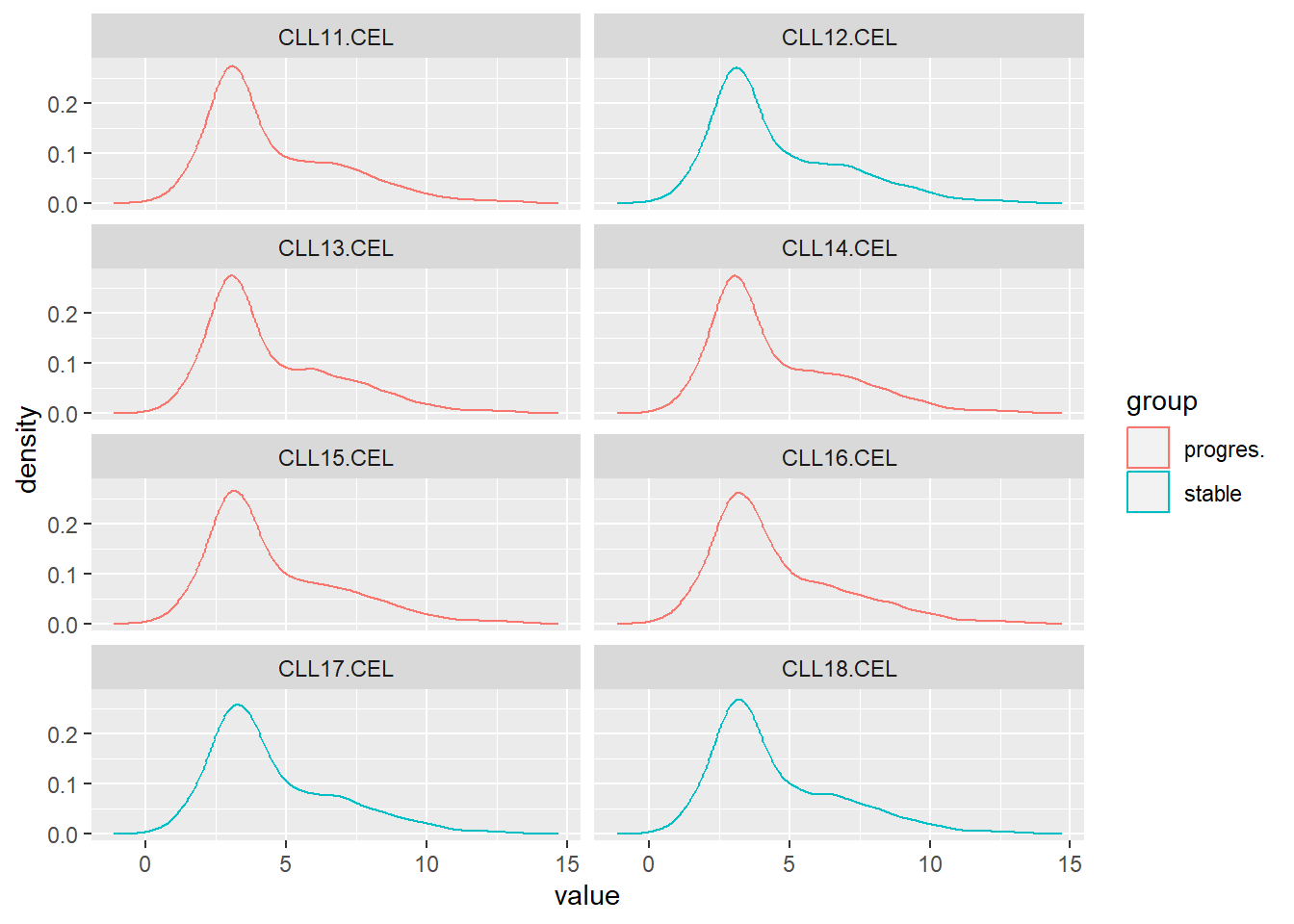
密度图(density)
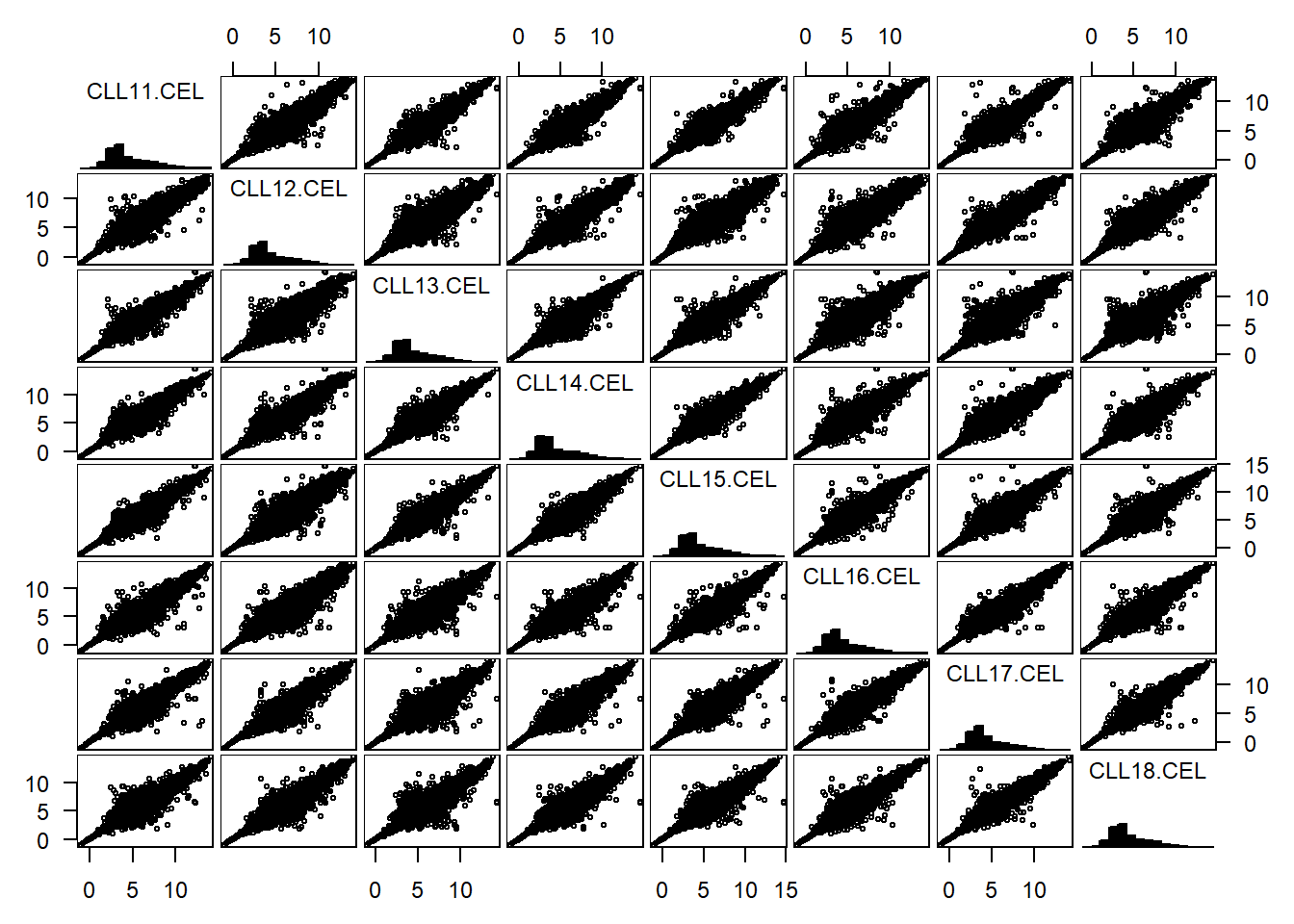
配对图(gpairs)
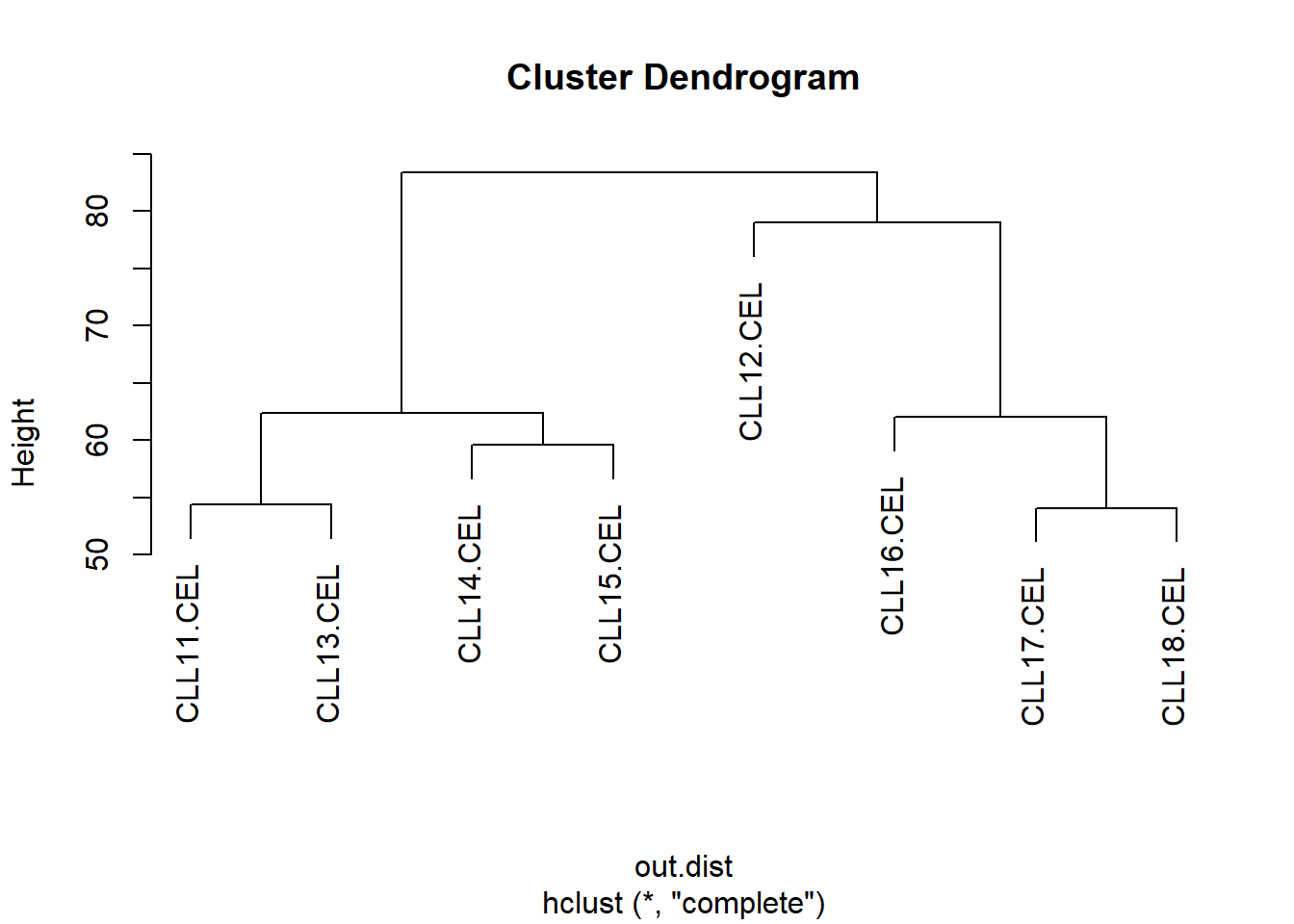
聚类图(cluster)
主成分分析(PCA)
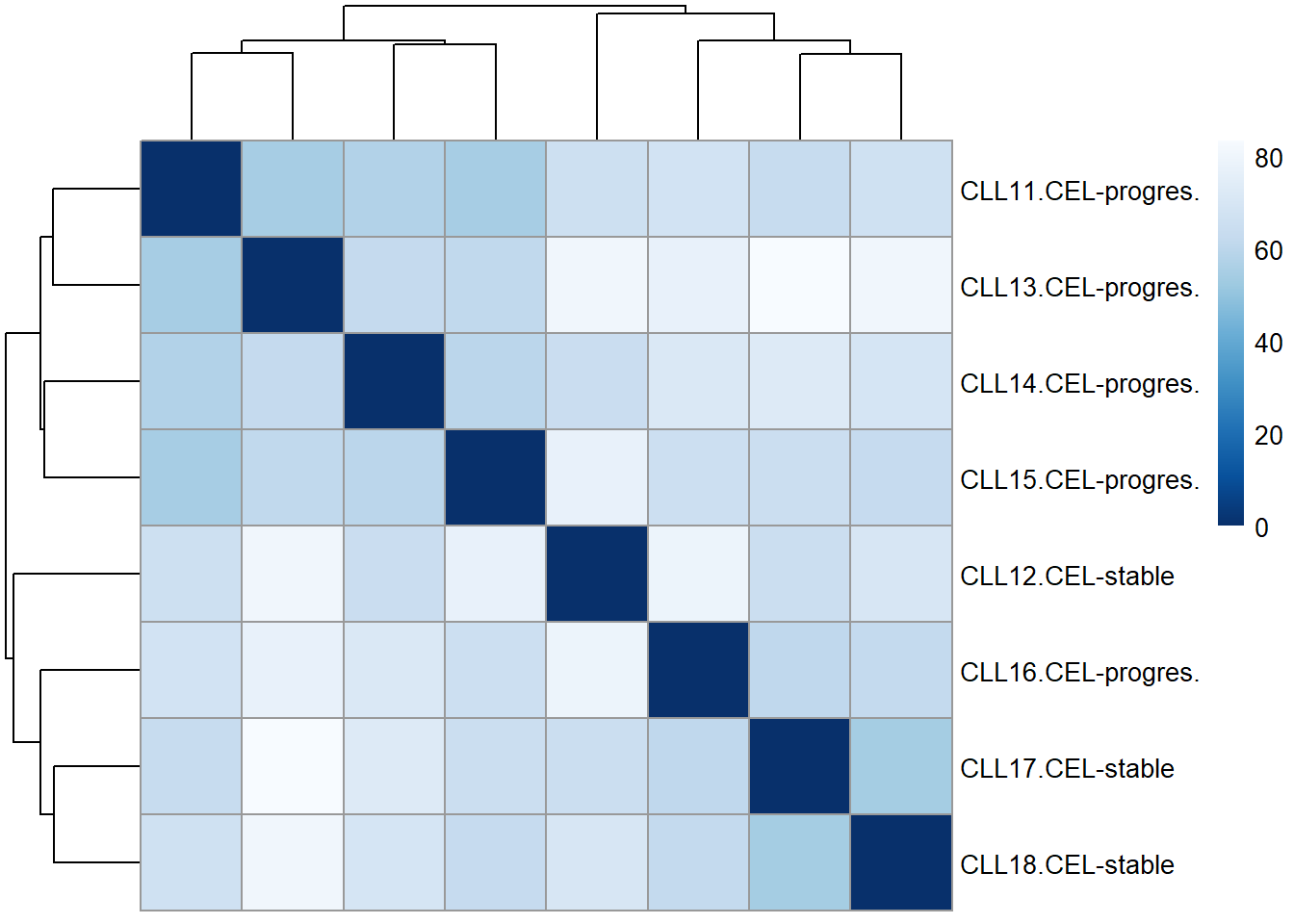
热图(heatmap)
火山图(volcano plot)
在绘制这些图形之前,首先需要先安装加载一系列包
if (! require ('corrplot' )) {install.packages ("corrplot" ); require ('corrplot' ) }if (! require ('gpairs' )) {install.packages ("gpairs" ); require ('gpairs' ) }if (! require ('vioplot' )) {install.packages ("vioplot" ); require ('vioplot' ) }if (! require ('tidyverse' )) {install.packages ("tidyverse" ); require ('tidyverse' ) }if (! require ('RColorBrewer' )) {install.packages ("RColorBrewer" ); require ('RColorBrewer' ) }#source("http://bioconductor.org/biocLite.R") if (! require ('CLL' )) {BiocManager:: install ("CLL" ); require ('CLL' ) }if (! require ('pheatmap' )) {BiocManager:: install ("pheatmap" ); require ('pheatmap' ) }if (! require ('limma' )) {BiocManager:: install ("limma" ); require ('limma' ) }
随后是加载绘图所需的表达矩阵数据。分析所用的表达矩阵数据对象(ExpressionSet obejct)由Affymetrix 的 AffyBatch 对象经 gcrma 处理后获得。
原数据为22组样本的12,625个基因表达状况,根据疾病状态分为两组:stable 或 progressive,此处仅选取前8个样本用作演示。
注 : gcrma是Bioconductor中一个与芯片数据处理相关的包,主要功能是利用序列信息调整背景.
data ("sCLLex" )<- sCLLex[,1 : 8 ] # 样本数过多,仅选取前8个 <- sCLLex$ Disease # 获取分组信息 <- exprs (sCLLex) # 获取表达矩阵 head (exprSet, n= 3 )
CLL11.CEL CLL12.CEL CLL13.CEL CLL14.CEL CLL15.CEL CLL16.CEL CLL17.CEL
1000_at 5.743132 6.219412 5.523328 5.340477 5.229904 4.920686 5.325348
1001_at 2.285143 2.291229 2.287986 2.295313 2.662170 2.278040 2.350796
1002_f_at 3.309294 3.318466 3.354423 3.327130 3.365113 3.568353 3.502440
CLL18.CEL
1000_at 4.826131
1001_at 2.325163
1002_f_at 3.394410
之后,还要利用tidyr::gather将原本的宽数据 重塑成长数据 。这一步被称之为数据规整化,是数据分析流程中至关重要的一步,详见Hadley所写的Tidy data 一章。当前数据存在问题是:列名(CLLxx.cCEL)应该是变量名,而这里却是变量的值。
<- as.data.frame (exprSet)$ probe <- row.names (exprSet)<- tidyr:: gather (exprSet, key= 'sample' ,value= 'value' ,CLL11.CEL: CLL18.CEL)$ group <- rep (group_List, each= nrow (exprSet))rbind (head (exprSet_L,2 ), tail (exprSet_L,2 ))
probe sample value group
1 1000_at CLL11.CEL 5.743132 progres.
2 1001_at CLL11.CEL 2.285143 progres.
100999 AFFX-YEL021w/URA3_at CLL18.CEL 3.651349 stable
101000 AFFX-YEL024w/RIP1_at CLL18.CEL 2.914602 stable
经过这基本处理,便能得到以探针,样本,处理结果和组别信息为列名的数据框。
完成了上述准备工作后,先用箱形图,小提琴图,柱状图,密度图了解各个样本表达数据的分布情况。
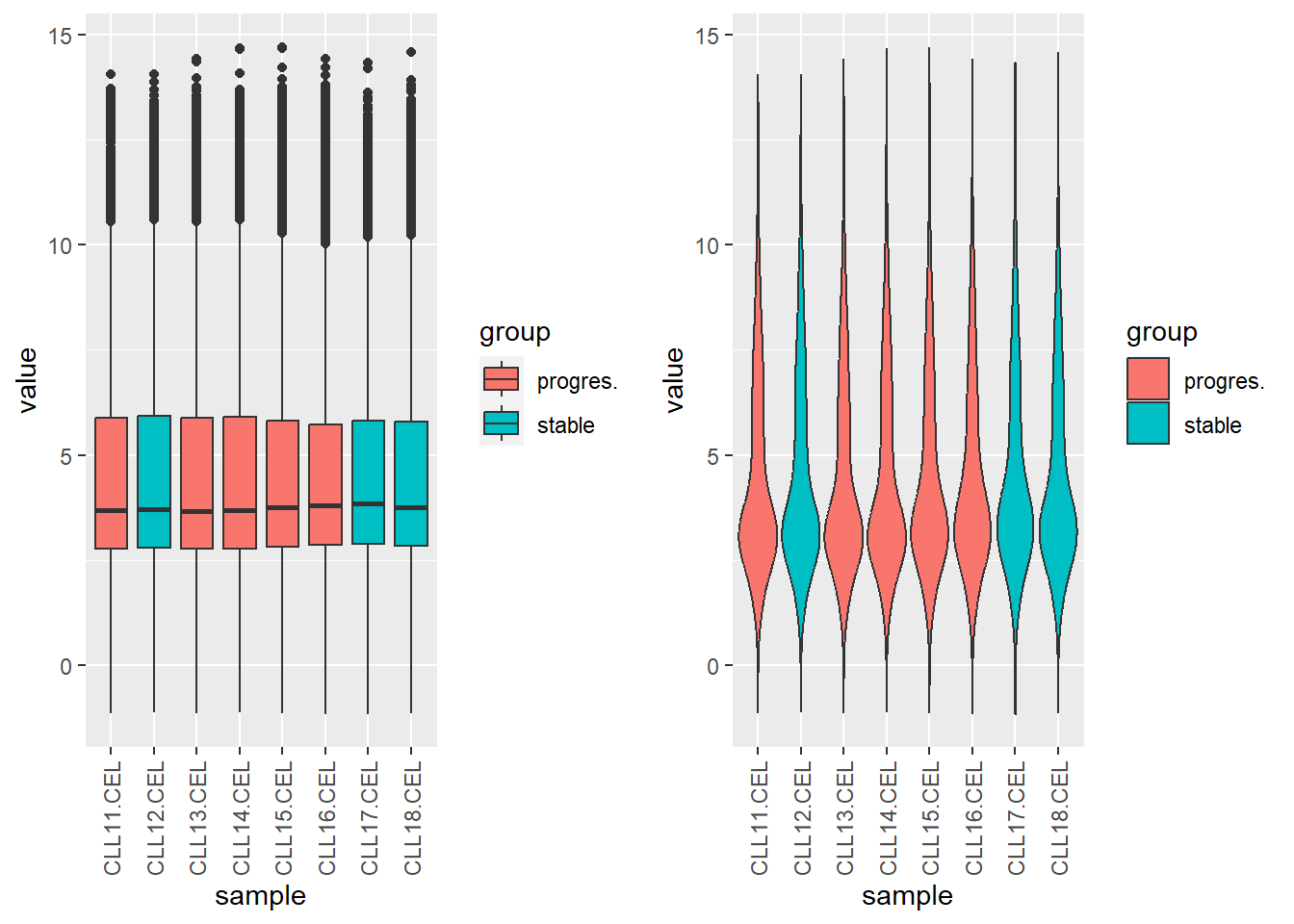
library (ggplot2)library (grid)grid.newpage ()pushViewport (viewport (x= 0 , width= 1 / 2 , just= "left" ))<- ggplot (exprSet_L,aes (x= sample,y= value,fill= group)) + geom_boxplot () + theme (axis.text.x = element_text (angle= 90 , hjust= 1 , vjust= .5 ))print (p1, newpage= FALSE )popViewport ()pushViewport (viewport (x= 1 / 2 , width= 1 / 2 , just= "left" ))<- ggplot (exprSet_L,aes (x= sample,y= value,fill= group)) + geom_violin () + theme (axis.text.x = element_text (angle= 90 , hjust= 1 , vjust= .5 ))print (p2, newpage= FALSE )
其中小提琴图可以认为是箱形图与核密度图的结合体。
library (ggplot2)# 条形图 <- ggplot (exprSet_L,aes (value,fill= group)) + geom_histogram (bins = 200 )+ facet_wrap (~ sample, nrow = 4 )print (p3)# 密度图 <- ggplot (exprSet_L,aes (value,col= group)) + geom_density ()+ facet_wrap (~ sample, nrow = 4 )print (p4)
这里使用了ggplot2的分面特性,fact_wrao()为每一个变量都绘制相应的图。如果不使用分面,还可以观察不同分组数据在同一幅图中的分布情况。
<- ggplot (exprSet_L,aes (value,col= group)) + geom_density () print (p5)
上面提及的四类图形描述的都是每一组样本各自的情况,而下面谈到的gpairs和cluster则是探索不同变量之间的关系。
配对关系图 :gpairs能够产生分组变量两两之间的关系。要求的输入数据为宽数据 ,即每列代表不同的细胞,每行表示不同的基因。
library (gpairs)gpairs (exprSet[,1 : 8 ]#,upper.pars = list(scatter = 'stats') #,lower.pars = list(scatter = 'corrgram')
聚类图 : 通过计算基因表达量之间的欧几里得距离,从而对不同样本进行分类。
= dist (t (exprSet[1 : 8 ]),method= 'euclidean' )= hclust (out.dist,method= 'complete' )plot (out.hclust)
热图(heatmap) : 本质上类似于散点图,只不过它利用颜色深浅表征数据的大小,以矩阵替代点。如果颜色表示为两个样本之间的距离,可以结合上面的聚类图,用来探索不同处理样本之间的差异。
<- as.matrix ( out.dist )rownames (sampleDistMatrix) <- paste (colnames (exprSet[1 : 8 ]), group_List,sep= "-" )colnames (sampleDistMatrix) <- NULL <- colorRampPalette ( rev (brewer.pal (9 , "Blues" )) )(255 )pheatmap (sampleDistMatrix,clustering_distance_rows = out.dist,clustering_distance_cols = out.dist,col = colors)
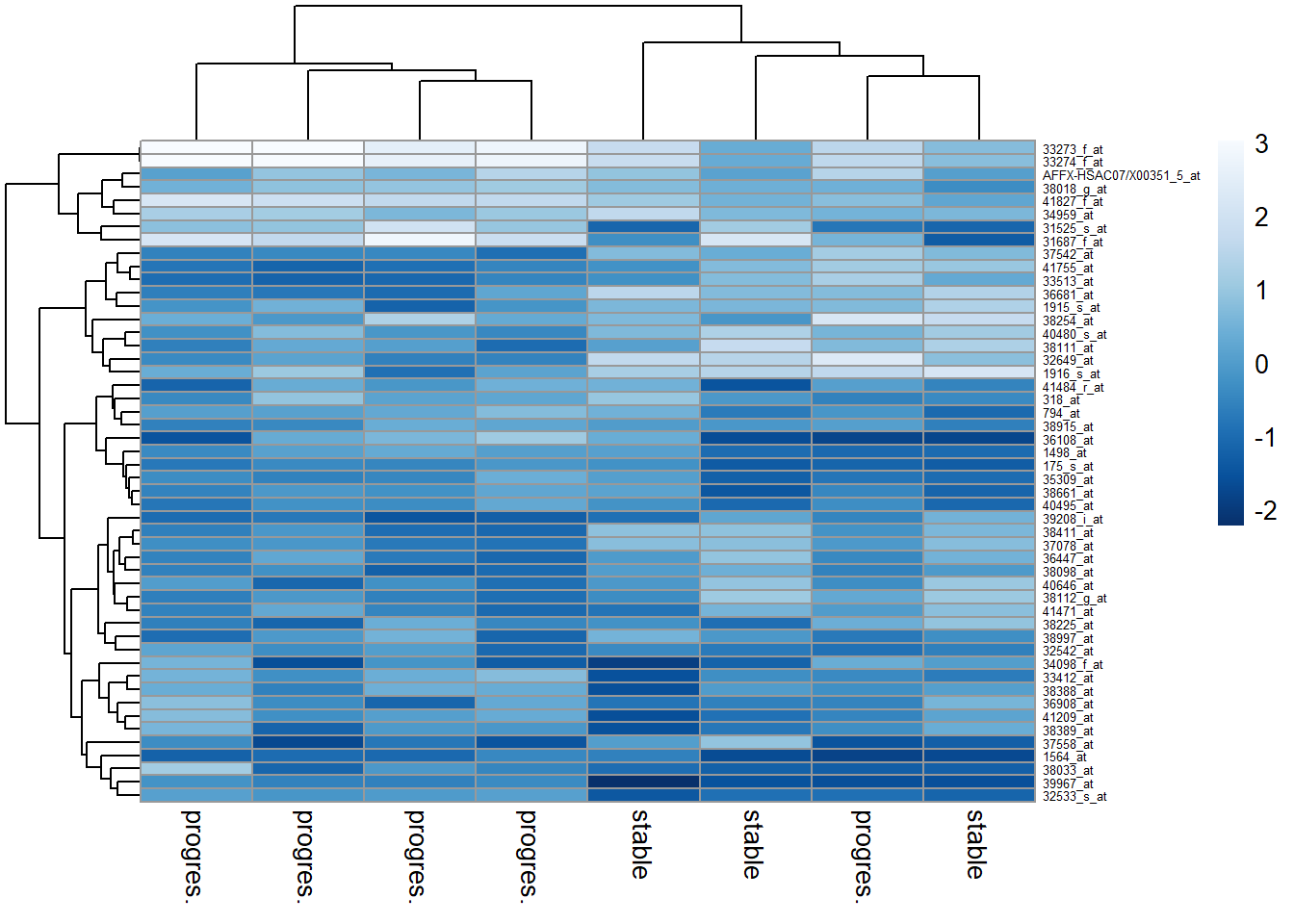
当然,也能用热图揭示不同样本间基因表达模式的差异,这里颜色就用来表征基因表达量。
# 选择表达量较高的基因 <- names (sort (apply (exprSet[1 : 8 ], 1 , mad),decreasing = T)[1 : 50 ])<- exprSet[choose_gene, ][1 : 8 ]<- scale (choose_matrix)# 使用pheatmap绘图 rownames (choose_matrix) <- rownames (choose_matrix)colnames (choose_matrix) <- group_List<- colorRampPalette ( rev (brewer.pal (9 , "Blues" )) )(255 )pheatmap (choose_matrix,col = colors,fontsize_row = 5 )
除了pheatmap,gplots包的heatmap.2()和自带的heatmap也能绘制热图。热图是否美观主要取决于整体配色。下图直观的表达了一个观点,合理的配色是可视化效果的加分项。
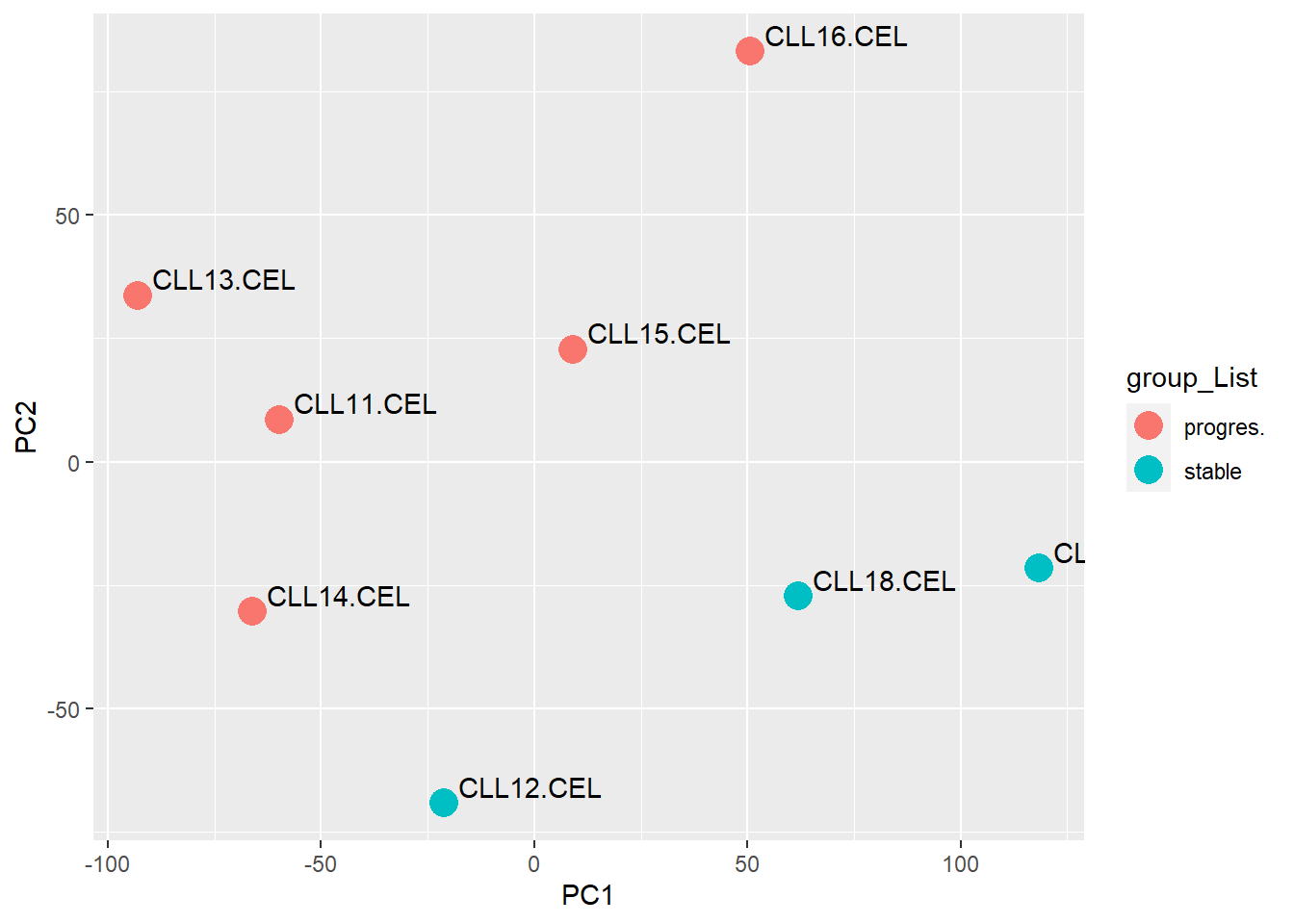
PCA : PCA本质是散点图,X和Y轴表示不同主成分,不同点之间的距离表示样本之间在两个主成分下的差异。
<- prcomp (t (exprSet[1 : 8 ]),scale= TRUE )<- data.frame (pc$ x)<- cbind (samples = rownames (pcx),group_List, pcx) <- ggplot (pcr, aes (PC1, PC2)) + geom_point (size = 5 , aes (color = group_List)) + geom_text (aes (label = samples),hjust = - 0.1 , vjust = - 0.3 )print (p)
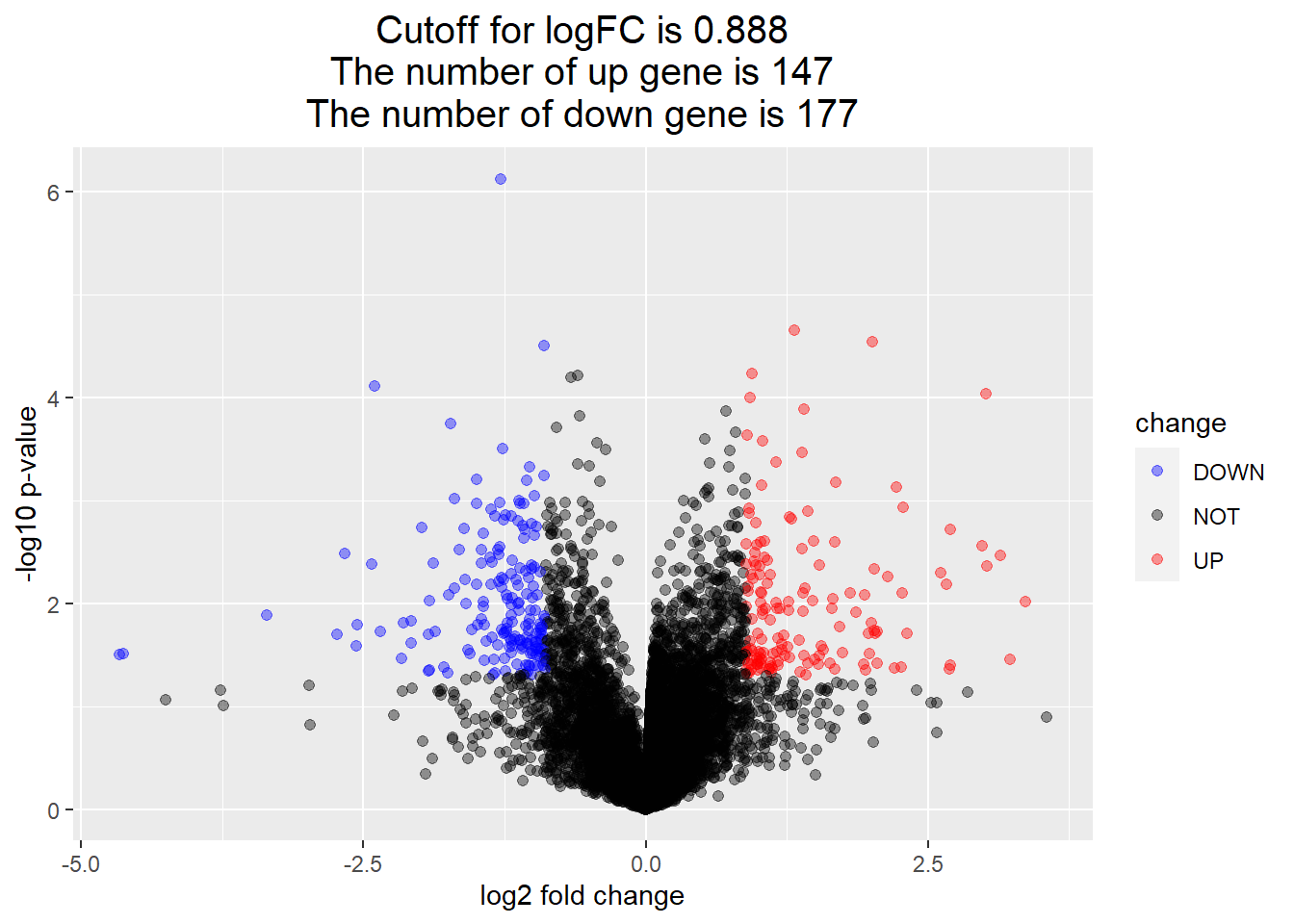
火山图 :火山图主要用在差异表达分析之后,用于直观地进行样本间差异基因筛选。本质上依旧是散点图,X轴表示取对数后的倍数变化(log2 Fold Change), Y轴则表示取对数后的显著性水平
<- model.matrix (~ factor (group_List))<- lmFit (exprSet[1 : 8 ],design)<- eBayes (fit)<- topTable (fit,coef= 2 ,n= Inf )with (DEG, plot (logFC, - log10 (P.Value), pch= 20 , main= "Volcano plot" ))
火山图既然本质上是散点图,那么只要以log2FC和-log10 pvalue 构建数据框,就可以使用 ggplot2 进行绘图,对目标区域进行高亮显示。
<- with (DEG,mean (abs ( logFC)) + 2 * sd (abs ( logFC)) )$ change <- as.factor (ifelse (DEG$ P.Value < 0.05 & abs (DEG$ logFC) > logFC_cutoff,ifelse (DEG$ logFC > logFC_cutoff ,'UP' ,'DOWN' ),'NOT' )<- paste0 ('Cutoff for logFC is ' ,round (logFC_cutoff,3 ),' \n The number of up gene is ' ,nrow (DEG[DEG$ change == 'UP' ,]) ,' \n The number of down gene is ' ,nrow (DEG[DEG$ change == 'DOWN' ,])<- ggplot (data= DEG, aes (x= logFC, y= - log10 (P.Value), color= change)) + geom_point (alpha= 0.4 , size= 1.75 ) + theme_set (theme_set (theme_bw (base_size= 20 )))+ xlab ("log2 fold change" ) + ylab ("-log10 p-value" ) + ggtitle ( this_tile ) + theme (plot.title = element_text (size= 15 ,hjust = 0.5 ))+ scale_colour_manual (values = c ('blue' ,'black' ,'red' )) ## corresponding to the levels(res$change) print (g)
转录本结构图
RNA转录翻译时存在可变剪切,因此同一个基因在不同时间和空间下会产生不同的转录本。GTF和GFF 在数据存放类型一章介绍过,用于注释基因组上的基因。
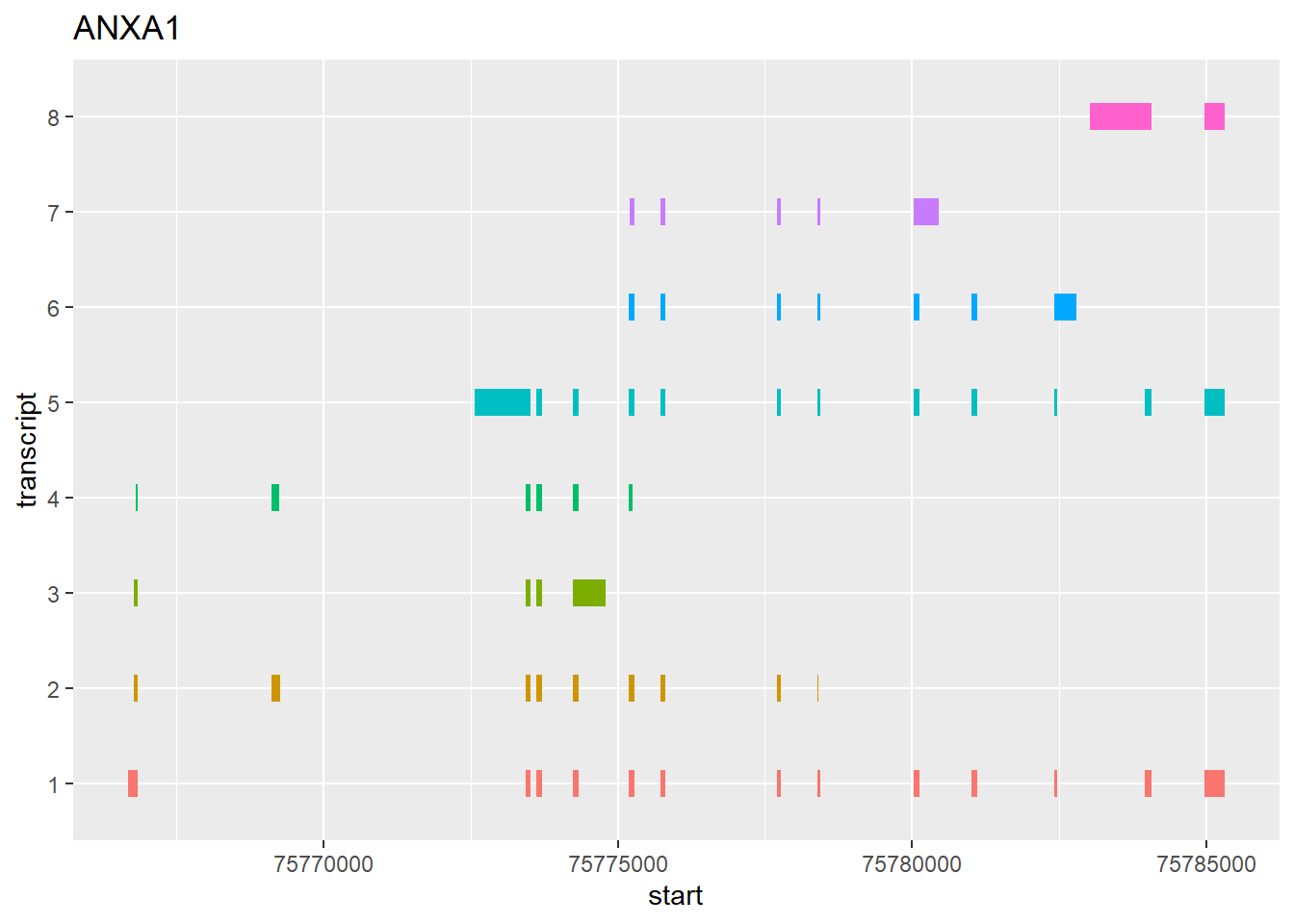
对转录本结构进行可视化的本质在于理解,Y轴用于区分不同的基因,X轴则表示染色体距离,以矩阵长度表示基因元件的起始和结束。因此,可以使用ggplot2根据GTF画基因的多个转录本结构
<- read.table ("data/gencode.v7.annotation_goodContig.gtf.gz" ,stringsAsFactors = F,header = F,comment.char = "#" ,sep = ' \t ' )<- gtf[gtf[,2 ] == 'HAVANA' ,]<- gtf[grepl ('protein_coding' ,gtf[,9 ]),] $ gene <- sapply (as.character (gtf[,9 ]), function (x) sub (".*gene_name \\ s([^;]+);.*" , " \\ 1" , x))<- 'ANXA1' <- gtf[gtf$ gene== draw_gene,c (1 ,3 : 5 )]names (structure) <- c ("chr" , "record" , "start" , "end" )<- which (structure$ record == "transcript" )<- idx+ 1 <- c (idx[- 1 ]- 1 , nrow (structure))<- lapply (seq_along (s), function (i) {<- structure[s[i]: e[i],]$ transcript <- i return (x)%>% do.call (rbind, .)<- g[g$ record == "exon" ,]$ transcript <- factor (g$ transcript)library (ggplot2)ggplot (g) + geom_segment (aes (x= start, xend= end, y= transcript, yend= transcript, color= transcript), size= 5 ) + theme (legend.position= "none" ) + labs (title= "ANXA1" )
Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.
reads覆盖图
由于染色体的物理特性,某些区域的测序深度会明显高于其他部分。reads覆盖图用于探索不同read在不同区域的覆盖情况。 其实本身原理很简单,就是把全基因组的每个坐标的depth都得到,然后得到depth的频数,然后画图。 我们可以对每条染色体单独来绘图,也可以针对全基因组来绘图。这里使用是我们存放在data文件下的wgs.bam。 脚本很简单:
samtools mpileup wgs.bam | perl -alne \ '{if($F[3]>100){$depth{"over100"}++}else{$depth{$F[3]}++}}END{print "$_\t$depth{$_}" foreach sort{$a <=> $b}keys %depth}' \
> wgs.depth.txt得到数据分为两列, 第一列是测序深度,第二列是在该测序深度下有多少个位点。因此第二列加起来就会是染色体的禅读。
<- read.table ('data/wgs.depth.txt' , stringsAsFactors = F)<- ggplot (a, aes (x= V1, y= V2)) + geom_line (lwd= 2 )<- p1 + geom_vline (xintercept = 27 ) + xlab ("测序深度" ) + ylab ("位点数" ) print (p2)